Mentz114
- 5,429
- 292
The single photon experiment of Grangier showed that if a phase shift ##\theta## is introduced in one arm of a Mach-Zehnder interferometer then there is interference when the two beams are recombined - even if only one photon is introduced.
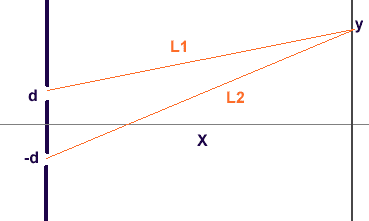
If a particle encounters a double slit of suitable geometry then one possibility becomes two which are recombined at some point on the screen. I wondered what the result would be if the phase difference in the MZ could be expressed in terms of the two slit geometry. This is easily done and the result is ##\theta_s=2\pi(L_1-L_2)/\lambda## where ##L_1^2=X^2+(y-d)^2,\ L_2^2=X^2+(y-2d)^2##.
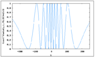
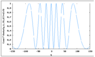
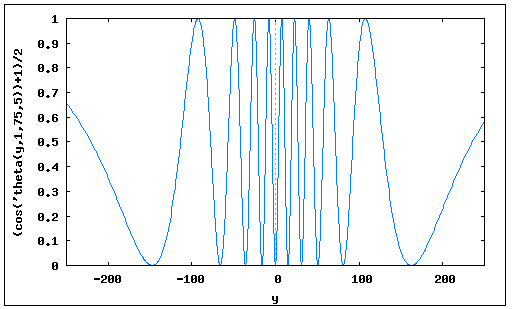
One of the detectors in the MZ setup has probability ##(1+\cos(\theta))/2 =\cos(\theta/2)^2##. Putting ##\theta_s## into this looks like this for X=75, λ=1, d=5
which at least looks plausible. I'm not sure if this is interesting or valid, but it is all quantum.
If a particle encounters a double slit of suitable geometry then one possibility becomes two which are recombined at some point on the screen. I wondered what the result would be if the phase difference in the MZ could be expressed in terms of the two slit geometry. This is easily done and the result is ##\theta_s=2\pi(L_1-L_2)/\lambda## where ##L_1^2=X^2+(y-d)^2,\ L_2^2=X^2+(y-2d)^2##.
One of the detectors in the MZ setup has probability ##(1+\cos(\theta))/2 =\cos(\theta/2)^2##. Putting ##\theta_s## into this looks like this for X=75, λ=1, d=5
which at least looks plausible. I'm not sure if this is interesting or valid, but it is all quantum.