- #1
Nezva
- 46
- 0
When linear operators A and B act on a function ψ(x), they don't always commute. A clear example is when operator B multiplies by x, while operator A takes the derivative with respect to x. Then
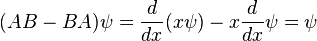
which in operator language means that
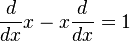
To get the last equation they divided through by ψ but why is it true? I guess what I'm trying to say is that the second equation makes no sense => d/dx*x - x*d/dx doesn't always equal 1... so why do they say that?
which in operator language means that
To get the last equation they divided through by ψ but why is it true? I guess what I'm trying to say is that the second equation makes no sense => d/dx*x - x*d/dx doesn't always equal 1... so why do they say that?