Optics Problems: Submerged light

[yuvlevental]

Homework Statement

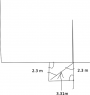
A green light is submerged 2.30 m beneath the surface of a liquid with an index of refraction 1.39. What is the radius of the circle from which light escapes from the liquid into the air above the surface?

Homework Equations

Critical angle: Sin(AngleCritical)=(n2/n1), n1>n2
Well I think...

The Attempt at a Solution

Is the radius a direct line of light from the light to the water's surface?
If so: sin-1(1.39/1) = 46 cos(46)*2.3=ans

 

[dynamicsolo]

You seem to have the critical angle correct. Draw a picture of the situation. The light source (which I take it you are to treat as a point) would have rays reaching the surface from 2.3 meters below. At the surface, the rays just at the critical angle which define the radius of this circle make a 46º angle to the perpendicular. What angle do they make to the line going straight up from the source to the surface? If the distance up to the surface is 2.3 m, what would the radius of the circle be?

 

[yuvlevental]

I got 3.31m, but I know that I am wrong. It the hypothenuse in the attatched picture the one that the problem meant?

 

[dynamicsolo]

I got 3.31m, but I know that I am wrong. It the hypothenuse in the attatched picture the one that the problem meant?

That sounds like you found the diameter of the circle. How did you calculate this value?

BTW, attachments can take hours to be cleared on this board. They should not be relied upon if you want a quick reply...

 

[yuvlevental]

i did 2.3/cos(46) to find the length between the point of light and where the light meets the water. Also, I did 3.31/2, but the answer is still wrong. I'm not sure what the circle is. Can you describe it to me?

 

[dynamicsolo]

i did 2.3/cos(46) to find the length between the point of light and where the light meets the water. Also, I did 3.31/2, but the answer is still wrong. I'm not sure what the circle is. Can you describe it to me?

You don't want the hypotenuse of the triangle, as that traces the ray of light itself. You are interested in the leg of the triangle perpendicular to the vertical leg, which is the distance along the surface of the water from the point directly above the light source. The other end of that leg is the point where the light ray traveling at the critical angle emerges from the water. What would be the length of that leg?

 

[yuvlevental]

thank you very much good madam/sir, you are my hero :-DDDDD