Saitama
- 4,244
- 93
Optics -- Refraction and a transparent sphere
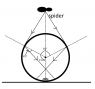
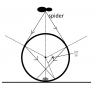
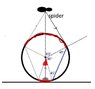
A spider is hanging by means of its own silk thread directly above a transparent fixed sphere of radius R=20 cm as shown in the figure. The refractive index of the material of the sphere is equal to ##\sqrt{2}## and the height of the spider from the centre of the sphere is 2R. An insect, initially sitting at the bottom, starts crawling on the sphere along a vertical circular path with the constant speed of ##\frac{\pi}{4}## cm/s. For how long time the insect will be invisible for the spider, assume that it crawls once round the vertical circle.
(see attachment)
Honestly, I have no idea. I don't have a clue about which equations I have to use here.
Any help is appreciated. Thanks!
Homework Statement
A spider is hanging by means of its own silk thread directly above a transparent fixed sphere of radius R=20 cm as shown in the figure. The refractive index of the material of the sphere is equal to ##\sqrt{2}## and the height of the spider from the centre of the sphere is 2R. An insect, initially sitting at the bottom, starts crawling on the sphere along a vertical circular path with the constant speed of ##\frac{\pi}{4}## cm/s. For how long time the insect will be invisible for the spider, assume that it crawls once round the vertical circle.
(see attachment)
Homework Equations
The Attempt at a Solution
Honestly, I have no idea. I don't have a clue about which equations I have to use here.
Any help is appreciated. Thanks!