MHB Optimize Definite Integral Function: Math Help | Yahoo Answers

[MarkFL]

Here is the question:

Math help please, I think it about trig.?


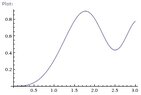
if g(x) = integral from 0 to x (sin(x^2)) on [0,3], then for what value g have a local minimum and for what value of x does g have a local maximum. plot the graph to verify your results.

I have posted a link there to this thread so the OP can view my work.

 

[MarkFL]

Hello Fourze,

We are given the function:

$$g(x)=\int_0^x\sin\left(t^2 \right)\,dt$$

Note: I have change the "dummy" variable of integration so that it is not the same as the upper limit. This is just considered good practice, to help avoid confusion.

So, we want to differentiate with respect to $x$, and equate the result to zero to obtain the critical numbers. We may do so using the derivative form of the FTOC:

$$g'(x)=\sin\left(x^2 \right)=0$$

Thus, we find:

$$x^2=k\pi$$ where $$k\in\mathbb{Z}$$

Since we are given $$0\le x\le3$$, we take the non-negative root:

$$x=\sqrt{k\pi}$$

On the given domain, this is:

$$x=0,\,\sqrt{\pi},\,\sqrt{2\pi}$$

Now, we may use the 2nd derivative test to determine the nature of $g(x)$ associated with the critical values.

$$g''(x)=2x\cos\left(x^2 \right)$$

$$g''(0)=0$$ No conclusion can be drawn.

$$g''\left(\sqrt{\pi} \right)<0$$ This is a local maximum.

$$g''\left(\sqrt{2\pi} \right)>0$$ This is a local minimum.

Hence, we find a local maximum at $x=\sqrt{\pi}$, and a local minimum at $x=\sqrt{2\pi}$.

Here is a plot of the function on its given domain:

View attachment 1858

In case you cannot view the attached plot, here is a link to the program used to produce the plot:

plot y=integral of sin(t^2)dt from 0 to x where x=0 to 3 - Wolfram|Alpha

 

[MarkFL]

I wanted to comment further about the critical value at $x=0$. Now, we can easily see that $g(x)$ is an odd function, since its derivative is even:

$$g'(-x)=-\sin\left(x^2 \right)=-g'(x)$$

Thus, we may conclude that at the critical value $x=0$, there is no relative or local extremum.

Consider the following:

$$\frac{d}{dx}\left(F(x) \right)=f(x)$$

Now, if $f(x)$ is even, we have:

$$\frac{d}{dx}\left(F(x) \right)=f(-x)$$

Now if we integrate:

$$\int\,d\left(F(x) \right)=-\int f(-x)\,-dx$$

$$F(x)=-F(-x)\implies F(-x)=-F(x)$$

We find the anti-derivative is odd.

And likewise if the derivative of a function is odd:

$$\frac{d}{dx}\left(F(x) \right)=f(x)$$

$$\frac{d}{dx}\left(F(x) \right)=-f(-x)$$

Now if we integrate:

$$\int\,d\left(F(x) \right)=\int f(-x)\,-dx$$

$$F(x)=F(-x)$$

We find the anti-derivative is even.