utsharpie
- 9
- 0
first, this is for my actual home's rooftop and isn't school related. I am not in a physics class.
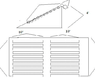
i have 2 areas of 10'X20' of gutters filled halfway with water on my inclined roof. the gutters are 10 feet long and have a radius of 2inches. each gutter is evenly placed one foot apart from the next as you go down from the top of the roof towards the ground. there are 2 of these 10'X20' each weighing 650lbs with combined plant weight side by side on a roof top that is 45'X25'.
the gutters will be connected to a counterbalance on the otherside of the rooftop. the distance from the point of the roof that the counterbalance can hang is a max of 2 feet. the roof top is 25 feet from the edge closest to the ground to the top of the roof and the height of the rooftop to the bottom edge of the roof closest to the ground is 4feet. i guess the angle is 35 to 40 degrees
i have 2 areas of 10'X20' of gutters filled halfway with water on my inclined roof. the gutters are 10 feet long and have a radius of 2inches. each gutter is evenly placed one foot apart from the next as you go down from the top of the roof towards the ground. there are 2 of these 10'X20' each weighing 650lbs with combined plant weight side by side on a roof top that is 45'X25'.
the gutters will be connected to a counterbalance on the otherside of the rooftop. the distance from the point of the roof that the counterbalance can hang is a max of 2 feet. the roof top is 25 feet from the edge closest to the ground to the top of the roof and the height of the rooftop to the bottom edge of the roof closest to the ground is 4feet. i guess the angle is 35 to 40 degrees