fadi_nzr
- 14
- 0
You have a sheet of paper that is 6 units wide and 25 units long placed
so that the short side is facing you. Fold the lower right hand corner
over to touch the left side. Your task is to fold the paper in such a way
that the length of the crease is minimized. What is the length of the
crease?
this what I have attempted so far
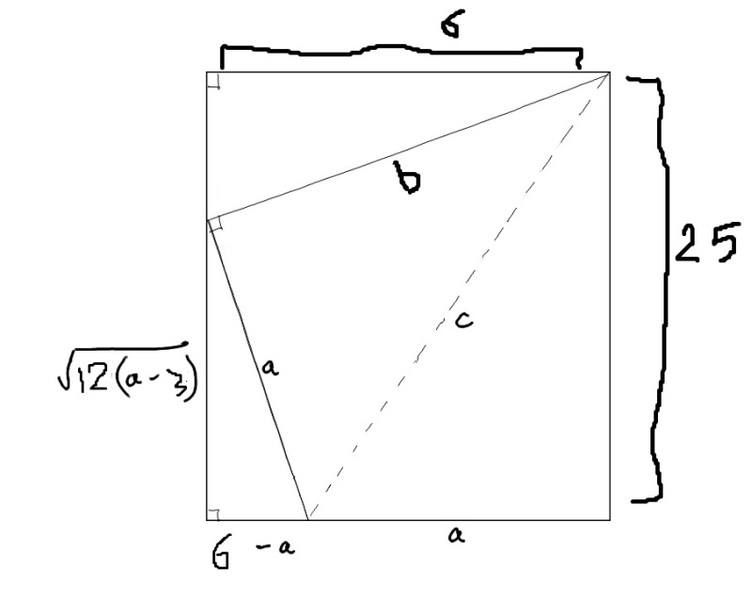
by proportions we get:
b/20 = a/sqrt(12a-36)
Solving for b. Use Pythagorean theorem to determine the length of c:
c^2 = a^2 + (36a^2)/(12a-36)
I am not sure if I am in the right track or not
any ideas or corrections
so that the short side is facing you. Fold the lower right hand corner
over to touch the left side. Your task is to fold the paper in such a way
that the length of the crease is minimized. What is the length of the
crease?
this what I have attempted so far
by proportions we get:
b/20 = a/sqrt(12a-36)
Solving for b. Use Pythagorean theorem to determine the length of c:
c^2 = a^2 + (36a^2)/(12a-36)
I am not sure if I am in the right track or not
any ideas or corrections