Our Beautiful Universe - Photos and Videos

[bruha]

Hi still one image (mybe little beter), at least more alike I found on net...

 

[davenn]

Hi still one image (mybe little beter), at least more alike I found on net...

yes definitely better focussed

Hopefully in a couple of years we will start seeing the Sun looking like the second image

 

[bruha]

 

[Devin-M]

Sunflower Galaxy - 29.3 million light years
72min of 2hr exposure - 36 x 2min - 1000mm f/10 - Bortle 2
Nikkor-Reflex focal 500mm f/5 + Nikon TC-201 2x teleconverter on Nikon D800

Center (RA, Dec):	(198.965, 42.031)
Center (RA, hms):	13h 15m 51.710s
Center (Dec, dms):	+42° 01' 51.521"
Size:	32.2 x 21.5 arcmin
Radius:	0.323 deg
Pixel scale:	1 arcsec/pixel

 

[Devin-M]

also fyi, the macro focusing rail works very well for getting the camera and lens balanced on the declination axis...

 

[DennisN]

I saw a couple of nice public lectures from the Royal Institution yesterday about black holes.
They covered many different aspects. A couple of things that are staggering is e.g. to imagine such massive objects as supermassive black holes spinning at such astounding speeds, and also the amount of energy released (and power) when black holes merge. It is mindblowing .

There was a series of nice comparison pictures and animations in the first lecture at 35 m 42 s and onwards.

The Physics of Black Holes - with Chris Impey


Q&A: The Physics of Black Holes - with Chris Impey


Black Holes and the Fundamental Laws of Physics - with Jerome Gauntlett

 

[Devin-M]

This little dongle will be my savior...

With my 600mm f/9 and 1000mm f/10 setups, its practically impossible to tell sometimes where I’m pointing through the view finder because the picture is so dark with such high aperature #’s, so I got a USB to Lightning adapter for transferring photos directly from my DSLR to my iphone photo library. From there I simply upload a test shot for plate solving to:

http://nova.astrometry.net/upload

...and it tells me exactly where I’m pointed. No more shooting for an hour and a half only to find out I was pointing at a completely different area of sky than intended.

Last night I had brought out my laptop, downloaded a pic from camera to laptop then airdropped to phone then uploaded to nova.astrometry.net/upload but my computer froze (literally, no pun intended) and wouldn’t restart til plugged in (I was a 30 minute drive from home in a bortle 2). I was about to order an inverter for my car to power the laptop but then I thought, why bother if I can go straight from DSLR into the phone.

It was almost sheer luck I was able to successfully aim the 1000mm setup at the sunflower galaxy last night without using plate solving.

 

[Devin-M]

another upgrade to help w/ pointing... green laser w/ telescope mount attached via macro focusing rail:

 

[chemisttree]

another upgrade to help w/ pointing... green laser w/ telescope mount attached via macro focusing rail:

View attachment 278343

Hmmm... Not how I imagined you would use that!

 

[Devin-M]

I will have 2 macro focusing rails... one for the laser and one to balance the whole camera on the declination axis via the lens mounting point.

 

[Devin-M]

Heart Nebula - IC 1805 - Sharpless 2-190 - 7500 light years
2hr exposure - 60 x 2min - 12800iso - 600mm f/9 - Moonlit Bortle 2 (2/20/21)
Nikon focal 300mm f/4.5 + Nikon TC-301 2x teleconverter
Nikon D800 w/ Star Adventurer 2i Equatorial Mount

Finally had a successful evening after many cloudy ones... I drove 30 miles to a Bortle 2 east of Redding, California, USA. The only downside was the moon was out and definitely affected the pictures. Tried out attaching the green laser to the camera for the first time and plate-solving with the plug from dslr to iphone ( http://nova.astrometry.net/upload ) -- I'd say it was revolutionary. I didn't even look through the viewfinder or at the live view at all. I figured out on the Stellarium app my phone where I wanted to point the camera, then aimed the green laser (after syncing the laser and camera on the north star), then took a test shot, downloaded to phone, plate-solved and adjusted till aim achieved. It was far easier than trying to look through the viewfinder and figure out where I'm pointed. Focused through Bahtinov mask, 40 darks & 40 flats. Took photos of the Heart Nebula and the Great Galactic Face in Markarian's Chain of galaxies.

Center (RA, Dec): (38.105, 61.368)
Center (RA, hms): 02h 32m 25.087s
Center (Dec, dms): +61° 22' 04.363"
Size: 2.52 x 1.68 deg
Radius: 1.513 deg
Pixel scale: 4.72 arcsec/pixel

 

[Devin-M]

Great Galactic Face - Markarian's Chain - M86 - M84 - NGC 4388 - NGC 4387 - 52 - 65 million light years
2hr exposure - 60 x 2min - 12800iso - 600mm f/9 - Moonlit Bortle 2 (2/20/21)
Nikon focal 300mm f/4.5 + Nikon TC-301 2x teleconverter
Nikon D800 w/ Star Adventurer 2i Equatorial Mount

Center (RA, Dec): (186.432, 12.801)
Center (RA, hms): 12h 25m 43.624s
Center (Dec, dms): +12° 48' 04.830"
Size: 40.6 x 27 arcmin
Radius: 0.406 deg
Pixel scale: 1.68 arcsec/pixel

 

[Oldman too]

Great detail on your info, thanks!

 

[DennisN]

I used 1/503 sec and the ISO that made that work on the moon.

I will definitely try with various settings the next time.

Moongazing/moon photo session:

Last evening/night I photographed the Moon and tried various new camera settings (shutter speeds 1/500 s and 1/1000 s at ISO 50, 100 and 200), along with new stacking settings and new editing in Photoshop.

Even though I only used my small monocular (diameter 40 mm), I got very pleased with the result.
It became the best photo of the Moon I've taken so far.

I guess I understand now why this hobby can be so addictive; over a long period of time you try, change things and then try again etc, in order to improve the results. And this time, when I saw the finished photo I felt very satisified. The next time I will try the same using my cheap 70 mm telescope instead of the monocular.

----------------------------------------------------------------------------------

Gear used: 40 mm monocular, tripod, LG G4 phone.
Photo settings: ISO 100, 1/1000 s shutter speed, DNG (uncompressed)
Stacking info: 25 stacked photos (50% of the photos), Drizzle 1.5 incl. Sharpening and 50% mix in of the original photos.
Software used: Open Camera (Android) -> PIPP -> AutoStakkert -> Photoshop
Photoshop edits: (1) increased contrast (2) Shadows/Highlights: increased highlights and increased midtone contrast (no editing of "Shadows") and (3) slight increase of vibrance

Here's the monocular I used, with a very technically advanced stray light shield made of black paper fastened with masking tape :

 

[Devin-M]

Markarian's Chain (of Galaxies) - M86 - M84 - NGC 4388 - NGC 4387 - 52 to 65 million light years
2hr exposure - 60 x 2min - 12800iso - 600mm f/9 - Moonlit Bortle 2 (2/20/21)
Nikon focal 300mm f/4.5 + Nikon TC-301 2x teleconverter
Nikon D800 w/ Star Adventurer 2i Equatorial Mount

I wanted to do a bit more processing than normal before posting this image. I edited out all the foreground stars so almost every point of light in the above image is an entire galaxy.

Full Frame w/ Stars:

Center (RA, Dec): (186.947, 12.897)
Center (RA, hms): 12h 27m 47.179s
Center (Dec, dms): +12° 53' 47.830"
Size: 3.01 x 2.01 deg
Radius: 1.810 deg
Pixel scale: 5.65 arcsec/pixel

 

[davenn]

With stars
looks totally weird without stars

 

[DennisN]

A friend just sent me a link to this STUNNING video.
Seeing a craft land on another planet, and filmed live, is just simply a-m-a-z-i-n-g.

Perseverance Rover’s Descent and Touchdown on Mars (Official NASA Video)

 

[Andy Resnick]

( http://nova.astrometry.net/upload )

Thanks for this link! I gave it a try with one of my images (downscaled to 33%, 8-bit TIFF) and it worked!

Thanks!

 

[Devin-M]

I gave it a try with one of my images (downscaled to 33%, 8-bit TIFF) and it worked!

I’ve started setting the quality setting on my dslr camera to capture both the RAW image and a low res jpg, so that while I’m trying to point the camera I can transfer the low res jpg from the dslr to iphone via the camera dongle, then upload to http://nova.astrometry.net/upload to find where I’m pointing, then I can adjust as needed til the aim is close to perfect. Also for plate solving, a 10 sec exposure is good enough, then when I’m pointed properly I crank the exposure time up to 2min, etc.

 

[Andy Resnick]

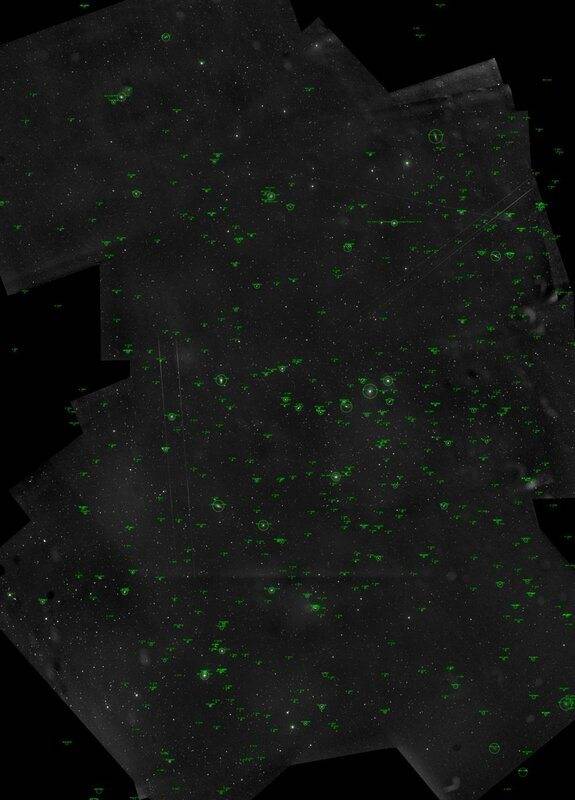
Whoa- the site managed to handle the full mosaic:

 

[Devin-M]

With stars
looks totally weird without stars

To me it looks like a lobster. M86, M84, NGC 4388, NGC 4387 are the face, NGC’s 4474, 4468, 4459 are the end of the tail, M87 & NGC 4371 are the claws. NGC 4402 is a raised eyebrow.

 

[Andy Resnick]

I second using nova.astrometry.net, it's a lot of fun to see how many deep sky objects it can find- here's one of the Leo Triplet-

But it failed to identify a small smudge near the Ring nebula (I marked it with a square)- it's present in the SDSS survey but not named...? Any guesses?

 

[Devin-M]

I would try cropping the image and inputting just that area...

 

[Andy Resnick]

Ah- Aladin to the rescue! It's LEDA 2029852, a galaxy:

http://simbad.u-strasbg.fr/simbad/sim-id?Ident=LEDA 2029852&NbIdent=1

 

[bruha]

Hello, still one sun green filt. image from today (sharpened and expos. adjusted with Gimp-I supose some granulation is recognizable ...

 

[chemisttree]

I can’t wait for solar activity to come back!
Today’s SOHO image...

 

[Andy Resnick]

Hello, still one sun green filt. image from today (sharpened and expos. adjusted with Gimp-I supose some granulation is recognizable ...

I can’t wait for solar activity to come back!
Today’s SOHO image...

What's that thing? Haven't seen it in months...

 

[chemisttree]

Hello, still one sun green filt. image from today (sharpened and expos. adjusted with Gimp-I supose some granulation is recognizable ...

Are you observing using an aperture mask or full aperture? Here is an example of an aperture mask. Discussion here.

 

[bruha]

Hello, I observing with full aperture, I don't know this way.. you mean put lit over Sun baader folie or just lit without folie?
Thanks,,,

 

[chemisttree]

You put the large cap on the tube, remove the small cap and place a solar filter over the small opening. Your Baader green filter would still go on your eyepiece.
You will need 1 more filter to cover the small aperture in the tube cap.

Do you currently not have a full aperture solar filter of some kind? ! If you don’t, we should talk before your next observation!