LCSphysicist
- 644
- 163
- TL;DR
- ..
I would appreciate if someone could help me to understand what is happening in section 12.3 from the Howard George's book.
First of all, the propose of the section is to show how $SU(3)$ decomposes into $SU(2) \times U(1)$. But i can't understand what is happening. First of all, i can't get the notation here: (where the dot is supposed to mean the trivial representation and the number notation at right of the boxes means $(2I+1)_Y$)
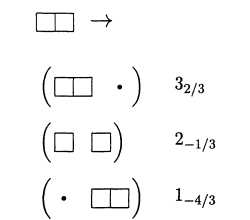
I can see that the two box in the same row represents a $6$ represetation of the $SU(3)$. But then, what just happens bellow? He goes on, and show another example
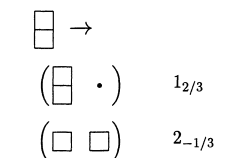
I am not sure what exactly these figures means. So the question can be summarized in two individual questions:1) What does the notations means? How do i get this decomposition? That is, what are the rules (I can understand Young tableaux rule, is something like that?) Why the first case above, for example, have $I=0,Y=2/3$?
2) How exactly this show to me that $SU(3)$ decomposes in $SU(2) \times U(1)$?... Just another example:
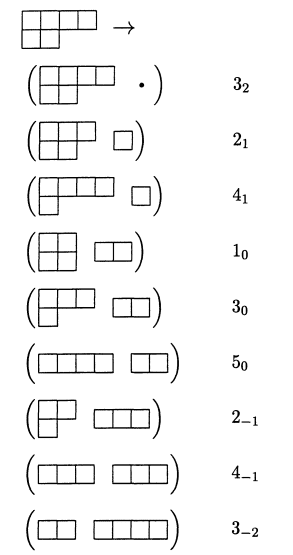
First of all, the propose of the section is to show how $SU(3)$ decomposes into $SU(2) \times U(1)$. But i can't understand what is happening. First of all, i can't get the notation here: (where the dot is supposed to mean the trivial representation and the number notation at right of the boxes means $(2I+1)_Y$)
I can see that the two box in the same row represents a $6$ represetation of the $SU(3)$. But then, what just happens bellow? He goes on, and show another example
I am not sure what exactly these figures means. So the question can be summarized in two individual questions:1) What does the notations means? How do i get this decomposition? That is, what are the rules (I can understand Young tableaux rule, is something like that?) Why the first case above, for example, have $I=0,Y=2/3$?
2) How exactly this show to me that $SU(3)$ decomposes in $SU(2) \times U(1)$?... Just another example: