Parallel and Series Capacitors?

[ilovephysics16]

In the figure below, a potential difference V = 150 V is applied across a capacitor arrangement with capacitances C1 = 12.0µF, C2 = 6.00µF, and C3 = 16.0µF. Find the following values.

Here's the diagram: http://www.webassign.net/hrw/hrw7_25-28.gif

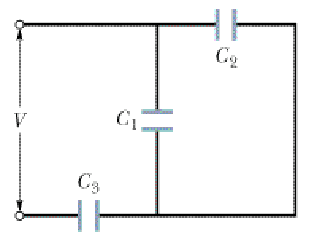
I already solved this problem but I'm having some trouble understanding the concept behind it. I know that capacitors 1 and 2 are in parallel and that they are in series with capacitor 3, but I don't understand why. Especially because capacitors 1 and 2 aren't parallel in the way I'm used to seeing parallel capacitors, like this: http://www.rapidtables.com/electric/capacitor/parallel capacitors circuit.GIF.

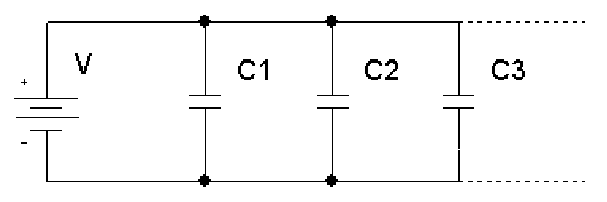
Also, if you combine 1 and 2 in parallel, what does the resulting capacitor even look like? I'm having trouble visualizing this. Can anyone help me understand this problem? I would really appreciate it.

 

[jtbell]

In your first diagram, mentally "slide" C₂ along its wire to the right and down onto the vertical section at the right side. That makes C₁ and C₂ look more like the "standard" parallel capacitor diagram. Then "bend" the wires and slide the wire junctions around a bit, without moving them through any capacitors or breaking any connections. You should be able to make it look like a "standard" series + parallel combination.

None of the manipulations above affect the equivalent capacitance of the circuit, nor do they affect the equivalent resistance in similar problems involving resistors, because they don't change the topology of the circuit. Just don't break any wires or move any components through a junction, or a junction through a component.

 

[ilovephysics16]

Got it. Thanks!

 

[epenguin]

I got a bit interested in capacitor networks because of the problems people were bringing here. Yes they often have problems through picturing them over-rigidly, the diagrams are abstract, topological, you can freely change them in a rubber sheet geometry way, i.e. with the limitations that jtbell has explained.

I think also many students end up with a purely formulaic rather than physical vision of these things based on remembering the series and parallel laws or formulae. I'm sure I did. Instead it is healthy to have some physics of it all in mind. For instance in your case the total charge on a C1 and C2 is the sum of the two charges. Because they are connected on both sides the potential across them is the same for both. So as capacitance is defined as ratio of charge to potential, sum divided by same thing, the total capacitance of 1 and 2 is the sum of the individual ones - general law for parallel capacitances.

Instead when capacitors are in series, (you have C3 in series with the effective capacitance C1 + C2) there is no adding up of charges, the charges on each capacitor is the same. Because the charge on each plate is equal in magnitude (though opposite in sign) to the plate facing it. What does add up is the potential across them of course. So same as before but the other way round, potential adds, charge same for each, this is a bit more difficult to see but V = Q/C, so for a series of potentials what adds up is not the charge - the only one that counts is one on an external plate,- but the 1/C 's. So the 1/C 's and up for capacitors in series the same way that 1/R 's add up for resistors in parallel.

Also I've found useful in solving more complicated problems to note that the conductively isolated part of the circuit has total charge 0 - that is, when charges are added algebraically, taking account of their signs. For example with two capacitors in series the isolated 'internal' plates have equal opposite charges, summing algebraically to 0. The total charge on the three connected isolated plates of your circuit is also algebraically 0. see Exercise with Capacitors