Parallel transportation of a vector along a closed triangle

[Manu_]

Hello everyone,

I am trying to solve exercise 7.21 in the "Hobson, Efstathiou, Lasenby, General Relativity. An introduction for physicists."
What is asked is to show that the parallel transportation of a vector, along a closed triangle on a 2-sphere, results in an vector orthogonal to the initial one. The triangle has 3 right angles:

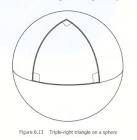
Here is what I tried so far: I have started with
\Delta v^{a} = -\frac{1}{2} R^{a}{}_{bcd} v^{b}_{P} \oint \! x^{c} \, d x^{d}

where \Delta v^{a} = v^{a}-v^{a}_{P} is the change underwent by the vector (the initial one being evaluated at point P), and R^{a}{}_{bcd} is the Riemann tensor.

The metric being ds^{2} = a^{2} \left( d \theta^{2} +\sin^{2}{\theta} d\phi^{2} \right) the only independant component of the Riemann tensor is R^{\theta}{}_{\phi \theta \phi} = -R^{\theta}{}_{\phi \phi \theta} = -R^{\phi}{}_{ \theta \theta \phi} = R^{\phi}{}_{ \theta \phi \theta} = \sin^{2}{\theta}

I then find:
\begin{split}<br /> \Delta v^{\theta} &amp;= -\frac{1}{2} R^{\theta}{}_{\phi \theta \phi} v^{\phi}_{P} \oint \! \theta \, d \phi -\frac{1}{2} R^{\theta}{}_{\phi \phi \theta} v^{\phi}_{P} \oint \! \phi \, d \theta \\<br /> &amp;= -\frac{1}{2} R^{\theta}{}_{\phi \theta \phi} v^{\phi}_{P} \left( \oint \! \theta \, d \phi - \oint \! \phi \, d \theta \right) \\<br /> \end{split}

And the closed path integrals are (A is the pole, B is the left vertex and B the right one):

\oint \! \theta \, d \phi = \int_{A}^{B} \theta \, d\phi + \int_{B}^{C} \theta \, d\phi + \int_{C}^{A} \theta \, d\phi

I then say that \phi does not vary from B to C, since we stay on the equator, so:

\oint \! \theta \, d \phi = \int_{A}^{B} \theta \, d\phi + \int_{C}^{A} \theta \, d\phi = \theta \left( -\frac{\pi}{2} +\frac{\pi}{2} \right) =0

And the other closed integral gives:

\begin{split}<br /> \oint \phi \! \, d \theta &amp;= \int_{A}^{B} \phi \, d \theta + \int_{B}^{C} \phi \, d \theta + \int_{C}^{A} \phi \, d \theta \\<br /> &amp;= \int_{B}^{C} \phi \, d \theta \\<br /> &amp;= \phi \times \frac{\pi}{2}<br /> \end{split}<br />

In the end, I obtain:

\Delta v^{\theta} = \frac{\pi}{4} \phi v^{\phi}_{P} \sin^{2}{\theta}

And by similar calculations, I get:

\Delta v^{\phi} = \frac{\pi}{4} \phi v^{\theta}_{P} \sin^{2}{\theta}

And from this, I was tempted to use the scalar product between the new vector (denoted with a prime) and the old one to see if they cancel:

\begin{split} v&#039;^{a}v_{a} &amp;= v&#039;^{\theta}v_{\theta} + v&#039;^{\phi}v_{\phi} \\<br /> &amp;= \left( v^{\theta}+\frac{\pi}{4} \phi v^{\phi}\sin^{2}{\theta} \right) v_{\theta} + \left( v^{\phi}+\frac{\pi}{4} \phi v^{\theta} \sin^{2}{\theta} \right) v_{\phi} \\<br /> &amp;= v^{\theta}v_{\theta} + v^{\phi}v_{\phi} + +\frac{\pi}{4} \phi \sin^{2}{\theta} \left(v^{\phi}v_{\theta} + v^{\theta}v_{\phi} \right)<br /> \end{split}<br />

which don't seem to cancel at all. Could anyone possibly point out my mistake(s)?

Thank you!
Manu

 

[TSny]

Here is what I tried so far: I have started with
\Delta v^{a} = -\frac{1}{2} R^{a}{}_{bcd} v^{b}_{P} \oint \! x^{c} \, d x^{d}

This equation is only valid for a very small loop. I don't see any way to apply it directly to the large triangle that you are working with. I would suggest using parallel transport around the triangle.