Parametric Equations of Keplerian Orbit

[derravaragh]

Homework Statement

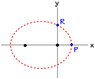
The figure illustrates a Keplerian orbit, with Cartesian coordinates (x,y) and
plane polar coordinates (r,φ).
F = -(G*M*m)/r^2
The parametric equations for the orbit:
r(ψ) = a ( 1 − e cos ψ)
tan(φ/2) = [(1+e)/(1-e)]^(1/2)* tan(ψ/2)
t(ψ) = (T/2π) ( ψ − e sin ψ)
where ψ is the independent, parametric variable; a, e, and T are constants.

Prove, directly from the parametric equations, that the angular momentum L is
constant. Express L in terms of the constants of the orbit (and any other relevant parameters).

Homework Equations

L = r x p
τ_net = r x F

The Attempt at a Solution

I know that in order for L to be constant, its derivative (net torque) must be 0, but this isn't really getting me anywhere. I know torque = rxF and L = rmv, but quite frankly I can't seem to figure out how to do this using the parametric equations.
What I have done using the parametric equations is this:
L = m*r(ψ)*v(t) = m*(a*(1-e*cos(ψ)))*v(t)
From here I'm having a difficult time finding an expression for v(t). I tried using the relations
ω=((2*π)/T) and v = ω*r for the following work:
t(ψ) = (1/ω)*(ψ-esin(ψ))
==> ω = (ψ-esin(ψ))/t(ψ)
==> ω = (ψ-esin(ψ))/((T/(2π))*(ψ-esin(ψ))
==> ω = (2π/T) (this obviously backtracked)
==> v = r*(2π/T)

∴L = m*(a*(1-e*cos(ψ)))*(a*(1-e*cos(ψ)))*(2π/T)
or L = m*a²*(1-e*cos(ψ))²*(2π/T)

I'm pretty sure this isn't right because it isn't going to be constant for different r values. Any help would be appreciated.

 

[mfb]

The time-derivative of L = r x p is not r x F. Don't forget that r depends on time as well.

L = rmv

Only if r and v are perpendicular to each other. In general, they are not.

 

[derravaragh]

Ok, well my intuition tells me to make L=r(psi)mvsin(θ) where θ is the angle between the positive x-axis and the line from the focal point to the point in the orbit

In my notes, we proved momentum was constant by making momentum L = m(x*v_y - y*v_x) and converting to polar coordinates. Does this equation apply to any elliptical orbit?

As for the time derivative of L = rmv, I am just unsure of how to do this as I can't seem to figure out the correct expression for v.

 

[mfb]

If you calculate the cross-product, this is exactly what you get. It looks tricky to get v_y, v_x based on the functions in the problem statement, however. L=r(psi)mvsin(θ) looks easier to evaluate.

As for the time derivative of L = rmv, I am just unsure of how to do this as I can't seem to figure out the correct expression for v.

The formula is wrong for an elliptic orbit anyway, there is no need to get v.

 

[vela]

The time-derivative of L = r x p is not r x F. Don't forget that r depends on time as well.

Yes, it is. When you apply the product rule, the other term drops out because dr/dt is parallel to p.

 

[mfb]

Oh, right.
Good, now it makes sense again (as $\dot{L}=\tau=r \times F$).

 

[derravaragh]

The formula is wrong for an elliptic orbit anyway, there is no need to get v.

Ok, I'm confused here. I'm continuing forward with L = mvr(ψ)sin(θ), but I don't understand why I don't need to get v, since v isn't constant? I know that when taking the time derivative of L one of the terms is r x p = 0 because they parallel

 

[vela]

From here I'm having a difficult time finding an expression for v(t). I tried using the relations
ω=((2*π)/T) and v = ω*r

These relations only give you one component of the velocity, due to the fact that the angle $\varphi$ is changing. The other component arises because $r$ varies with time.