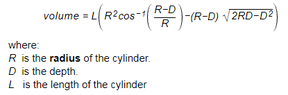MHB Partial Volume of a Cylinder Calculation

Click For Summary
SUMMARY

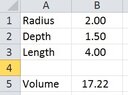
The discussion focuses on calculating the partial volume of a cylinder using a specific formula in Excel. The formula provided is V=L*(R^2*ACOS((R-D)/R)-(R-D)*SQRT(2*R*D-D^2), where V represents volume, L is the length, R is the radius, and D is the depth. Users expressed challenges in implementing this formula in Excel, particularly with the ACOS function. The conversation highlights the importance of understanding the order of operations and suggests using named cell ranges for clarity.

PREREQUISITES
  • Understanding of basic geometry, specifically cylinder volume calculations.
  • Familiarity with Excel formulas and functions, particularly ACOS and SQRT.
  • Knowledge of order of operations in mathematical expressions.
  • Experience with named ranges in Excel for improved formula readability.
NEXT STEPS
  • Research how to implement the ACOS function in Excel for accurate calculations.
  • Learn about named ranges in Excel to enhance formula clarity.
  • Explore the mathematical principles behind the volume of a cylinder.
  • Investigate troubleshooting common Excel formula errors related to trigonometric functions.
USEFUL FOR

This discussion is beneficial for Excel users, engineers, and students who need to calculate the partial volume of a cylinder and seek to enhance their understanding of Excel's mathematical functions.

CivCalc
Messages
2
Reaction score
0
It's been a long time since I've attended school, over 33 years ago. So my question may seem basic to many here. I wish to calculate the partial volume of a cylinder for my excel spreadsheet project. The formula I've found is attached. (unable to type it)

But I do not fully understand this formula. Particulalry the R sq cos -1 section. Could somebody please explain how I use cos
Thank You

View attachment 7715
 

Attachments

  • Formula.PNG
    Formula.PNG
    3 KB · Views: 150
Mathematics news on Phys.org
Hello, and welcome to MHB! (Wave)

I don't use Excel, but I imagine it would be something like:

Code: 
V=L*(R^2*ACOS((R-D)/R)-(R-D)*SQRT(2*R*D-D^2))
 
Thanks for response. No doesn't work on excel but that's OK, I'll investigate further
 
CivCalc said:
Thanks for response. No doesn't work on excel but that's OK, I'll investigate further

The Basic Spreadsheet
View attachment 7728
B1:B3 are the desired input values.

The formula in B5
View attachment 7729
I added a few sets of parentheses to emphasize order of operations.

You COULD name the cell ranges and refer to their meanings, rather than the cell addresses.
 

Attachments

  • Spreadsheet1.jpg
    Spreadsheet1.jpg
    8.6 KB · Views: 138
  • Spreadsheet2.jpg
    Spreadsheet2.jpg
    5.8 KB · Views: 132
Yeah, I figured what I gave was correct. :)
 

Similar threads

Cylinder Calculator - Volume Area Radius Height
  • · Replies 8 ·
Replies
8
Views
8K
Calculating 3D Cylinder Volumes & Areas With Constants
  • · Replies 14 ·
Replies
14
Views
3K
Propagation of Uncertainty - Hollow Cylinder
  • · Replies 1 ·
Replies
1
Views
4K
Undergrad Desorption probability calculation
  • · Replies 1 ·
Replies
1
Views
1K
Calculating Volume of Arbitrary Cross-Section Triangles
  • · Replies 17 ·
Replies
17
Views
4K
How Do You Calculate Geometric Buckling for Cylinders and Spheres?
  • · Replies 2 ·
Replies
2
Views
2K
Undergrad Atmospheric Density vs Altitude in an O'Neil Cylinder
  • · Replies 1 ·
Replies
1
Views
3K
Motor calculation for a rotating platform
  • · Replies 7 ·
Replies
7
Views
5K
High School Having trouble deriving the volume of an elliptical ring toroid
  • · Replies 4 ·
Replies
4
Views
4K
Can you solve the volume of a cube with unequal heights?
  • · Replies 67 ·
3
Replies
67
Views
37K