Particle moving from one potential to another

[gionole]

Homework Statement

..

Relevant Equations

..

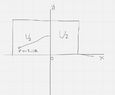
Attaching the image of the problem as an image. Somehow text is not copied from the book.

Somehow, I can't imagine the picture in my head. We can do it in 2D plane. I know, it mentions the solution, but need to see the drawing, otherwise, my logic fails.

I thought that maybe, first half space where we got $U_1$ constant, we draw it in $x<=0$ and 2nd half space when $x>0$ and I guess we treat instanteneous movement from first to second half space. I get it that since $x=0$ still belongs to first half space, on the whole $y$ axis, potential energy doesn't change and still is $U_1$. But when particle moves into 2nd one, definitely, force would act on $y$ direction, making momentum change.

Would appreciate if you could draw a picture of where angles are, half spaces, normal and so on.

 

[Gordianus]

Can you attach a drawing that shows the half spaces , the particle and its velocity?

 

[gionole]

Can you attach a drawing that shows the half spaces , the particle and its velocity?

`Well, the book doesn't show the drawing, only explains it with words as you can see on my attached image already. If you mean the drawing of my perception, I'm attaching it here. It doesn't mean it's correct.I presume at $x=0$, it's still the first half space's field($U_1$).

 

[Gordianus]

Nice drawing. Now think how the change in potential energy affects the particle's motion (Newton again)

 

[gionole]

Nice drawing. Now think how the change in potential energy affects the particle's motion (Newton again)

I mean when particle is at $x=0, y=k$ ($k$ doesn't matter what it is), potential energy is still $U_1$. But as soon as particle moves from $x=0$ to $x>0$, potential energy changes. Let's say particle was $x=0, y=5$ and moved to $x=0.0000000...1, y=5.000000001$, that means potential energy changes in both ($x$ and $y$) which means force acted on it in both directions which means momentum changes in both $x$ and $y$. $\vec F = \frac{d\vec p}{dt}$.

But the book says momentum is conserved in $y$ direction. how ?

 

[DrClaude]

I mean when particle is at $x=0, y=k$ ($k$ doesn't matter what it is), potential energy is still $U_1$. But as soon as particle moves from $x=0$ to $x>0$, potential energy changes. Let's say particle was $x=0, y=5$ and moved to $x=0.0000000...1, y=5.000000001$, that means potential energy changes in both ($x$ and $y$) which means force acted on it in both directions which means momentum changes in both $x$ and $y$. $\vec F = \frac{d\vec p}{dt}$.

But the book says momentum is conserved in $y$ direction. how ?

The change in $y$ has nothing to do with the change in potential. A better way to say it is that $dU/dy = 0$ everywhere.

 

[gionole]

I might get why dU/dy = 0, but was looking for the drawing of what the angles are. I know you can explain it with words, but drawing would be better.

 

[Gordianus]

Let's say U1>U2, can you add the force to the drawing?

 

[vanhees71]

In this kind of (only apparently simple academic problems) you must read the entire math in terms of distributions. Let's assume the plane separating the half-spaces is the $(12)$-plane of a Cartesian coordinate system. Then
$$U(x,y,z)=U_1 \Theta(-z) + U_2 \Theta(z),$$
where $\Theta(z)$ is the Heaviside unitstep function. Obviously the force is
$$\vec{F}=-\vec{\nabla} U=-(U_2-U_1) \delta(z) \vec{e}_z.$$
So you have to find a solution for
$$m \ddot{\vec{x}}=\vec{F}$$
with the initial condition $\vec{x}(0)=\vec{x}_0$ with $z_0<0$ and $\vec{v}(0)=\dot{\vec{x}}(0)=\vec{v}_0$ with $v_{0z}>0$, such that it moves from the lower to the upper half-space.

The only challenge is of course the $z$-component:
$$\ddot{z}=-(U_2-U_1) \delta(z).$$

 

[gionole]

Let's say U1>U2, can you add the force to the drawing?

If so, I know what you're gonna say. Force must then be in $+x$ direction. I get that, but I was asking why not in $y$ direction ? but I think intuitively, I'm feeling why.

@vanhees71 I appreciate your contributions to all the posts I'm making, but I want to say that sometimes, your explanations are complex to me. I was only meaning $x,y$ plane, then why do you show $z$ ? what's (12) ? Do you mean the separation of these 2 half spaces is not instanteneous - as if there is something between these 2 spaces ? I think it's instanteneous.

 

[vanhees71]

According to the problem it's a 3D problem with a potential having one value in one half-space and another in the other half-space. The first step in solving the problem is to map the question properly into math. That's why I started choosing a Cartesian coordinate system and defining the plane dividing the space into the two half-spaces as the (12)- or $(xy)$ plane defined by this coordinate system.

 

[haruspex]

The suddenness of the transition is irrelevant. You can treat it as a standard ballistics question (SUVAT), writing $mgh=\Delta U$.

 

[Ibix]

I was asking why not in $y$ direction ?

Do you know what is the expression for the force on a particle at position $(x,y)$ moving in some potential $V(x,y)$?

 

[Mister T]

I might get why dU/dy = 0, but was looking for the drawing of what the angles are. I know you can explain it with words, but drawing would be better.

The angles can't be shown on the diagram you drew. The reason is because your drawing doesn't show the arrows that represent the vectors $\vec{v}_1$ and $\vec{v}_2$.