Partition Function for system with 3 energy levels

[MigMRF]

Homework Statement

A system contains 3 particles A, B and C. A can have the energies (0, Delta) while B and C can have the energies (0,Delta,6 Delta). Determine the partition function if the particles and distinguisable. Then determine the partition function if the particles are indistinguishable

Relevant Equations

Z=sum(e^(-beta*E))

I determined the partition function of the particle A, B and C.

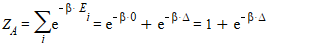
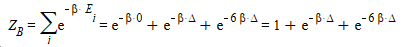
C should be the same as B.
I then considered the situation, where all particles are in the system at the same time, and drew a diagram of all possible arrangements:

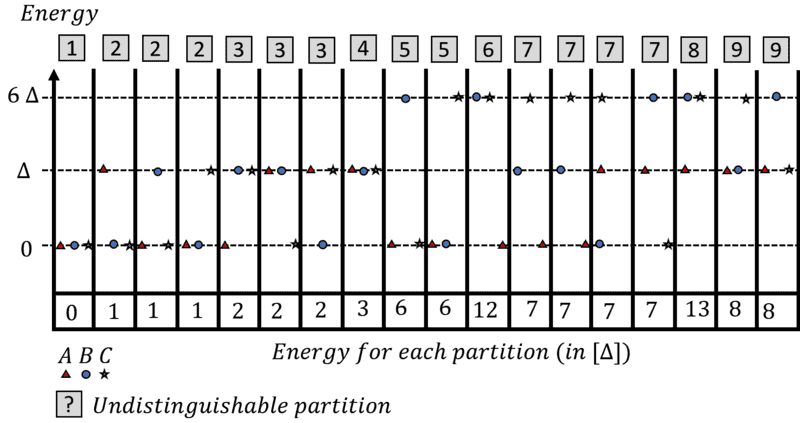
The grey boxes are the different partitions, given that we can't tell the difference on the particles. The number at the bottom of the table is the sum of all the energies.
From this table i created the two partition functions as shown below:
Distinguishable:

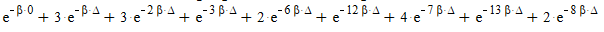
Indistinguishable:

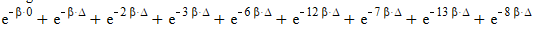
The correct answer is the following partition functions:

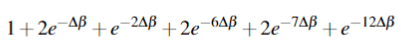
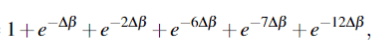
So my question is. Why does my method not work?

Kind Regards

 

[TSny]

I agree with your answer for part (a). It looks like the given solution does not include any states where particle A is in the state with energy $\Delta$.

For part (b), I'm not sure. When the particles are indistinguishable, we can no longer pick out "particle A" and restrict it to the first two energy levels, while allowing the other two particles to be in any of the three levels. This would be treating one of the particles differently than the other two, which doesn't make sense if the particles are indistinguishable. But, maybe they intend for us to interpret the restriction for part (b) as saying that the level with energy $6 \Delta$ is only allowed to hold at most two particles. So, we disallow the state where all three particles occupy this energy level. This appears to be how you interpreted it. If this is what they want, then I agree with your answer for part (b). It looks like their answer leaves out states where there are no particles in the lowest energy level.