Pendulum with Spring: Finding Position and Period

[Calabi_Yau]

Homework Statement

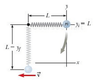
A system consists of a spring with force constant k = 1250 N/m, length L = 1.50m, and an object of mass m = 5.00kg attached to the end. The object is placed at the level of the point of attachment with the spring unstretched, at position yi= L, an then is released so that it swings like a pendulum.
a) Find the y position of the object at the lowest point.
b) Will the pendulum's period be greater or less than the period of a simple pendulum with same mass m and length L?

The Attempt at a Solution

b) As the spring will stretch out during the swing, its period will be greater than that of a simple pendulum, as the greater the l, the greater the period.

a) This is where I'm having trouble. I imagine the spring going down and stretching out to the max at the lowest point, and the shrinking again in the ascent.

I used an xy axis, with y = L being the plane of the mass before moving. The - Y would be the y coordinate at the lowest point.

I am not even sure if that is correct, but I took it and went on to tackle the problem with an energy approach.

Its maximum potential energy was at the top. U = mgL.
At the lowest point, Elastic potential energy is at its maximum Uelastic = 1/2 * k( Y)^2. And so is kinetic energy. This is where I get stuck. I don't now what to use for velocity. Because it has tangential and normal direction and has the length of the spring is not constant I don't know what to take into account for the normal direction.

This all should work if and only if my first assumptions were right, that the maximum length happens at the lowest point. But I'm not even sure about it.

Any help would be appreciated :)

 

[physicsboy121]

Let's say you slowly and steadily placed the object onto the spring, how much will it compress? This will be your new equilibrium point for the spring-object system.

 

[haruspex]

(a) sounds impossibly hard. How do we know that it won't fall into a rhythm whereby the mass follows a sort of W shape, the spring's elongation oscillating at four times the frequency of the pendulum? To be sure, we'd have to solve the equations of motion exactly, which is impossible for such large amplitudes.
However, if we assume no such frequency matching, so that subsequent motion is fairly chaotic, we can ask what is the lowest point it might reach at some time. You have conservation of work, but you need one more equation.
At the lowest point, what will the vertical speed be? Assuming that is in the middle of the swing, what relationship do you get between the speed and the extension of the spring?

 

[Calabi_Yau]

Can I use simple pendulum equations for the tangential velocity? Because after all, the tangential component of the force is the same as if it were a simple pendulum, and I can't figure out any other way to find the tangential component as I don't know the motion equations.

As with the radial component of the velocity, assuming the spring reaches its max enlongation at the bottom, it's radial speed will be ωA. With ω = √k/m and A = Y. Right?

 

[haruspex]

Can I use simple pendulum equations for the tangential velocity? Because after all, the tangential component of the force is the same as if it were a simple pendulum, and I can't figure out any other way to find the tangential component as I don't know the motion equations.

You can't use the usual SHM equation for a pendulum for two reasons. First, the amplitude is too great to approximate sin θ as θ. Secondly, the pendulum here varies in length.

As with the radial component of the velocity, assuming the spring reaches its max elongation at the bottom, its radial speed will be ωA. With ω = √k/m and A = Y. Right?

Why would ω = √k/m at the bottom?

Assuming that is in the middle of the swing, what relationship do you get between the speed and the extension of the spring?

Scratch that - what I was thinking of doesn't work.
It seems intuitive that there will be a minimum value the horizontal speed can take at the times when the mass is directly below the point of suspension. More generally, if the horizontal displacement is x then some formula like $ax^2+b\dot x^2 > c$. But I cannot think of a basis for finding what that minimum is.
(Of course, if that intuition is wrong, you can simply take the object to be instantaneously at rest at the lowest point and solve the energy equation. But from there on the mass would simply bob up and down, which seems most unlikely.)
You can write down the general energy equation, but I see no prospect of solving it.
I don't see any way to use momentum either. There's a variable force from the top with both horizontal vertical components, and the gravitational force has a variable moment about the point of suspension.
I hope to see the solution of this eventually - it will be intriguing.

 

[Calabi_Yau]

I think the solution won't be much complicated as the problem is on Serway's Physics for Scientists and Enginneers. I guess, I'll skip this one for a while and get back to it later.

If you come up with something, or if I come up with something I'll post it.

 

[TSny]

Here's the figure from Serway. The figure appears to show the mass moving horizontally at the bottom (θ = 0). This would not be true in general.

However, if the spring doesn't stretch very much during the swinging, then the velocity will be approximately horizontal at the bottom and the mass can be thought of as moving approximately on the arc of a circle at the bottom. You can check that the spring is pretty stiff. Hanging the mass on the end would only stretch the spring by about 2.6%.

Under this approximation you can set up energy and centripetal force equations to get an approximate solution. I find that the answers using this approximation agree pretty well with answers obtained from numerically integrating the equations of motion: about 2.4% error in y_f and about 0.29 % error in v at the bottom, if my calculations are correct.

 

[haruspex]

I just plotted it up in a spreadsheet. It seems that the numbers given have been carefully chosen so that the trajectory is quite simple. It swings symmetrically, with the side-to-side oscillation having twice the period of the stretch/contract oscillation. Maybe if you write out the differential equations and look specifically for a solution of that form it all drops out, but I still think that's a long shot.
If you analyse the vertical oscillation of the spring and the horizontal oscillation of the pendulum separately (at, say, equilibrium length for the vertical position), maybe they'll give the 2:1 period ratio, but I hardly think that's valid. The interactions could lead to a completely different result.

 

[haruspex]

the mass can be thought of as moving approximately on the arc of a circle at the bottom.
Under this approximation you can set up energy and centripetal force equations to get an approximate solution.

That was what I was hinting at in my first post, but retracted because I couldn't justify the arc-of-circle assumption. Looks like the critical parameter is kl/mg. When this is large (it's about 40 here), it probably is near enough.
It looks very different with smaller ratios. E.g. at 0.77 it gets very lopsided. When the mass is back at the original height, the spring is only half the length on one side as when it's on the other. When in the vertical position, there is still some vertical velocity.

 

[TSny]

Right, when the ratio kl/mg is considerably smaller than for the given data, you get some interesting motion.

 

[haruspex]

Right, when the ratio kl/mg is considerably smaller than for the given data, you get some interesting motion.

Here are graphs for kl/mg = 0.77

 

[TSny]

That looks like what I'm getting. Here's a case where I changed k to 200 N/m so that kL/(mg)≈ 6.1.

Too bad the problem is an even numbered problem, so no answer in the back. It would be interesting to see the textbook's answer.