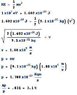Percent uncertainty of momentum

[dangsy]

Homework Statement

The position and momentum of a 1KeV electron are simultaneously determined. If its position is located to within 1Angstrom (Δx), what is the PERCENTAGE of uncertainty in its momentum?

Homework Equations

ΔxΔp >= h(bar)/2

The Attempt at a Solution

Δx = 1A = 1x10^-10m
Δp>= h(bar)/2Δx
Δp = 1.055x10^-34(kg/m^2)/s
-------------------------
2(1x10^-10m)
= 5.275x10^-25 kgm/s

how do I get the percentage of uncertainty?

 

[Shooting Star]

($\Delta$p/p)100.

Use the energy to find p.

 

[dangsy]

Thanks!

Here's what I did...
(I don't know how to use latex =/ )

KE = 1/2 mv^2
1 x10^3 eV = 1.602 x10^-16 J
1.602 x10^-16 J = 1/2 (9.1 x10^-31 kg) (v^2)
Sqrt[(2 (1.602 x10^-16 J))/(9.1 x10^-31 kg)] = v
v = 1.88 x10^7 m/s
p = mv
p = (9.1 x10^-31 kg) (1.88 x10^7 m/s)
p = 1.708 x10^-23 Kgm/s
Δp/p = .031 = 3.1 %

or click the attachment=)