Crusaderking1
- 158
- 0
Physics--distance using vectors.
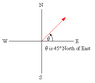
An explorer in the dense jungles of equatorial Africa leaves his hut. He takes 40 steps at an angle 45 degrees north of east, then 83 steps at an angle 60 degrees north of west, then 50 steps due south. Assume his steps all have equal length. Save him from becoming hopelessly lost in the jungle by giving him the displacement, calculated using the method of components, that will return him to his hut.
What is the magnitude of the displacement that will return the explorer to his hut?
What is the direction of the displacement that will return the explorer to his hut?
AxcosangleA =x-component
AysinangleA = y-component
The problem is not the math, the problem is that I need help finding the angles I'm suppose to be measuring. I'm never sure which angle or how to find the measurement of half the angles.
Ax = (40.0)(cosign 45) = 28.28
Ay = (40.0)(sin 45)= 28.28
bx =(83.0)(cosign 60) = -41.5
by =(83.0)(sin 60) = 71.9
cx =(50.0)(cosign ?) =
cy=(50.0)(sin ?) =
Then I know how to find magnitude, but I don't know the angles. Thanks!
Homework Statement
An explorer in the dense jungles of equatorial Africa leaves his hut. He takes 40 steps at an angle 45 degrees north of east, then 83 steps at an angle 60 degrees north of west, then 50 steps due south. Assume his steps all have equal length. Save him from becoming hopelessly lost in the jungle by giving him the displacement, calculated using the method of components, that will return him to his hut.
What is the magnitude of the displacement that will return the explorer to his hut?
What is the direction of the displacement that will return the explorer to his hut?
Homework Equations
AxcosangleA =x-component
AysinangleA = y-component
The Attempt at a Solution
The problem is not the math, the problem is that I need help finding the angles I'm suppose to be measuring. I'm never sure which angle or how to find the measurement of half the angles.
Ax = (40.0)(cosign 45) = 28.28
Ay = (40.0)(sin 45)= 28.28
bx =(83.0)(cosign 60) = -41.5
by =(83.0)(sin 60) = 71.9
cx =(50.0)(cosign ?) =
cy=(50.0)(sin ?) =
Then I know how to find magnitude, but I don't know the angles. Thanks!
Last edited: