J.live
- 95
- 0
Homework Statement
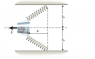
A horizontal slingshot consists of two light, identical springs (with spring constants of 74 N/m) and a light cup that holds a 1-kg stone. Each spring has an equilibrium length l0 = 49 cm. When the springs are in equilibrium, they line up vertically. Suppose that the cup containing the mass is pulled to x = 0.6 m to the left of the vertical and then released.
The Attempt at a Solution
ME= PE +KE
Initially PE = 1/2kx^2 KE= 0 --> ME = 1/2kx^2 +0 ---> 1/2(74)(.6)^2 +0 ?
Idk how to find the velocity. I am guessing we'll just use ME= 0+1/2mv^2 ?
Or, do I have to incorporate the equilibrium length into the equation somehow?
Any help will be appreciated.
Attachments
Last edited: