cpcolts
- 3
- 0
Here's an attachment.
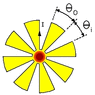
A poor artist might approximate a flower as a series of straight lines and arcs such as that shown below. We could caracterize the flower by specifying the inner and outer radii, and the inner and outer angles (shown). If a current I flows around along the lines and arcs, a magnetic field may be generated at the center of the figure. For the figure as drawn, please answer each of the following questions.
Will there be a magnetic field at the center?
If there is a field, would increasing the number of "petals" make the field bigger? Smaller? No effect?
If there is a field, and with the other variables fixed, will increasing Router make the field bigger? Smaller? No effect?
If there is a field, and with the other variables fixed, would making outer bigger and inner smaller make the field bigger? Smaller? No effect?
A poor artist might approximate a flower as a series of straight lines and arcs such as that shown below. We could caracterize the flower by specifying the inner and outer radii, and the inner and outer angles (shown). If a current I flows around along the lines and arcs, a magnetic field may be generated at the center of the figure. For the figure as drawn, please answer each of the following questions.
Will there be a magnetic field at the center?
If there is a field, would increasing the number of "petals" make the field bigger? Smaller? No effect?
If there is a field, and with the other variables fixed, will increasing Router make the field bigger? Smaller? No effect?
If there is a field, and with the other variables fixed, would making outer bigger and inner smaller make the field bigger? Smaller? No effect?