Rijad Hadzic
- 321
- 20
Homework Statement
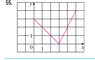
Hello I uploaded a picture of the image.
Find an expression for a function who's graph is the given curve.
Homework Equations
The Attempt at a Solution
The first function [0,3] y= -x+3 and the second one is y=2x-6 from 3 to 5
what I don't get, is why isn't the second one [3,5], instead the answer is (3,5)..
The way I see it at that point, x=3, it can be anyone of those equations...