- #1
rdn98
- 39
- 0
A picture has been included for your viewing pleasure.
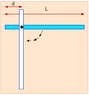
A stick of uniform density with mass M = 7.7 kg and length L = 0.6 m is pivoted about an axle which is perpendicular to its length and located 0.16 m from one end. Ignore any friction between the stick and the axle.
=======================
a) What is the moment of inertia of the stick about this axle?
The stick is held horizontal and then released.
b) What is its angular speed as it passes through the vertical
c) What is its angular acceleration as it passes through the vertical position?
d) What is the magnitude of the vertical component of the force exerted by the stick on the axle when the stick passes through the vertical?
=============
part a) Not too bad. I used the parallel axis theorem, and ended up with the correct answer of .38192 kg*m^2
b) Not too bad either. Used energy of conservation where mgh=.5I*w^2
where w is omega, and I is moment of inertia.
Got correct answer of 7.4379 rad/s
c) Now I'm stuck. I know that the forumula for calculating net torque is:
NetTorque=I*alpha
I know what (I) is, alpha I don't know, but I don't know how to calculate torque though for this problem. I know that in general, torque = r*F sin phi
So I need some help figuring out this torque business. :p
part d) Also stuck. Not sure really what to do here. :p
A stick of uniform density with mass M = 7.7 kg and length L = 0.6 m is pivoted about an axle which is perpendicular to its length and located 0.16 m from one end. Ignore any friction between the stick and the axle.
=======================
a) What is the moment of inertia of the stick about this axle?
The stick is held horizontal and then released.
b) What is its angular speed as it passes through the vertical
c) What is its angular acceleration as it passes through the vertical position?
d) What is the magnitude of the vertical component of the force exerted by the stick on the axle when the stick passes through the vertical?
=============
part a) Not too bad. I used the parallel axis theorem, and ended up with the correct answer of .38192 kg*m^2
b) Not too bad either. Used energy of conservation where mgh=.5I*w^2
where w is omega, and I is moment of inertia.
Got correct answer of 7.4379 rad/s
c) Now I'm stuck. I know that the forumula for calculating net torque is:
NetTorque=I*alpha
I know what (I) is, alpha I don't know, but I don't know how to calculate torque though for this problem. I know that in general, torque = r*F sin phi
So I need some help figuring out this torque business. :p
part d) Also stuck. Not sure really what to do here. :p