Why Are My Strain Values Displayed Incorrectly on the X-Axis in Excel?

[Saladsamurai]

I am trying to plot s stress-strain diagram using the tabulated data in the accompanying diagram below.

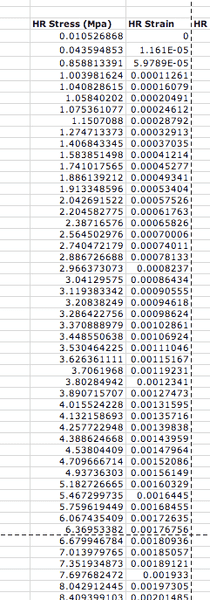
Now, notice that the values of strain (which will go on the x-axis) are very low--they range from 0.00001 to 0.23.

Now look at the graph ("I used an x-y scatter" with stress column as the Y data and strain as the X data) and you can see that the x-axis values are huge! (They range to 5500!)

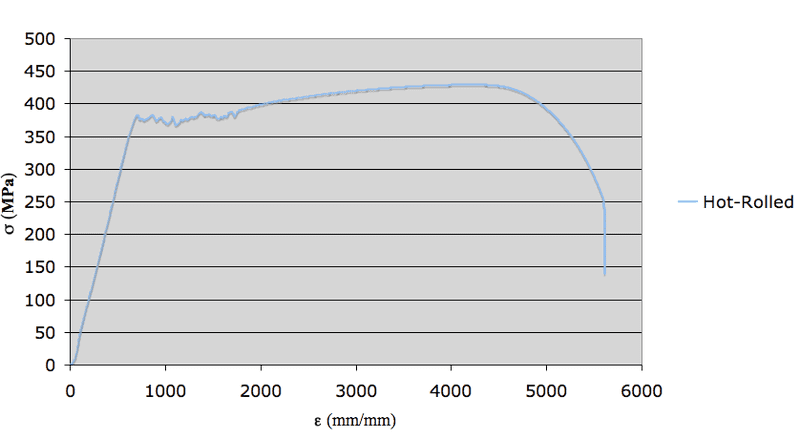
What am I doing wrong here?

 

[Saladsamurai]

Really...no one knows how to use excel?

 

[stewartcs]

Casey, I can't see you graphs. Can you insert them in a post instead (my company blocks the site that hosts the links).

CS

 

[Saladsamurai]

I got it. But I have another quick question. If I have my stress-strain data plotted and I want to find approximate values of where the proportional yield is, i.e., where the graph stops being 'linear', is there a way to calculate that with excel rather than "eyeballing it" using the curve?

 

[stewartcs]

I got it. But I have another quick question. If I have my stress-strain data plotted and I want to find approximate values of where the proportional yield is, i.e., where the graph stops being 'linear', is there a way to calculate that with excel rather than "eyeballing it" using the curve?

I believe you can calculate the slope (based off of your table values) which should be constant over the linear portion. Then, when the slope deviates you'll be in the non-linear region.

CS

 

[Saladsamurai]

Right, but how can I efficiently find where it deviates? I have 5600 values for each substance.

 

[stewartcs]

Right, but how can I efficiently find where it deviates? I have 5600 values for each substance.

I'm not sure if Excel has a function for that. You would have to approximate where the non-linearity ends and use the SLOPE function to calculate it the slope over that region. I can't think of anything else at the moment. Do you have the data set in Excel already? If so, zip it and attach it and I'll see if I can find a function that might work.

CS

 

[Saladsamurai]

Thanks stewart. I just approximated it using the graph. I am pretty sure that is what he wants us to do... I was just being a.r. :)

Here's another one though!: If I am to find out how much WORK is done on a specimen up until the proportional limit (through the elastic region) how would I do that?

I know that W=\int F(x)dx But how would I find out what F(x) is? It cannot be constant.

I know it is in the elastic region. So it must satisfy Hooke's Law. So I know that

F(x)=ax+c and I have plenty of data... so I guess I DO have F(x)...

Just one thing though. Is it F(x)=ax+c or F(x)=-ax+c

Thanks for your help too!

 

[stewartcs]

Thanks stewart. I just approximated it using the graph. I am pretty sure that is what he wants us to do... I was just being a.r. :)

Here's another one though!: If I am to find out how much WORK is done on a specimen up until the proportional limit (through the elastic region) how would I do that?

I know that W=\int F(x)dx But how would I find out what F(x) is? It cannot be constant.

I know it is in the elastic region. So it must satisfy Hooke's Law. So I know that

F(x)=ax+c and I have plenty of data... so I guess I DO have F(x)...

Just one thing though. Is it F(x)=ax+c or F(x)=-ax+c

Thanks for your help too!

Since you have the stress and strain data the work will be equal to the area under the curve (in the elastic region). Take a look at your graph in the elastic region, it should look like a triangle. Then finding the area of the triangle is trivial. Alternatively, Hooke's law would apply to the elastic region and after integrating you would have W = 1/2*k*x^2.

Hope this helps.

CS