You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
AI Thread Summary
The discussion revolves around difficulties in plotting a figure related to graphene distribution using Mathematica, specifically regarding the function g(ω²). The original poster struggles with errors in their code and questions the validity of the article's equations. Several users point out that the plotting should be done with respect to ω rather than ω² and highlight issues with the elliptic integral's argument. Despite attempts to clarify and assist, the original poster insists on the existence of a bug in Mathematica or the article, while others successfully reproduce the figure, emphasizing the importance of following guidance provided. The conversation underscores the need for careful attention to mathematical definitions and coding practices in computational tools.
Physics news on Phys.org
NascentOxygen
Staff Emeritus
Science Advisor
Homework Helper
- 9,248
- 1,080
Hi vesta33. http://img96.imageshack.us/img96/5725/red5e5etimes5e5e45e5e25.gif
Is there a question or something you intended should accompany your post?
Not that I will be able to help, but someone else may offer to ...
Is there a question or something you intended should accompany your post?
Not that I will be able to help, but someone else may offer to ...
Last edited by a moderator:
DrClaude
Mentor
- 8,477
- 5,693
I'll bite.NascentOxygen said:Is there a question or something you intended should accompany your post?
Not that I will be able to help, but someone else may offer to ...
You realize that ##g(\bar\omega^2)## is defined by different equations depending on the value of ##\bar\omega^2##? And that the figure in the paper plots ##g(\bar\omega^2)## as a function of ##\bar\omega^2##, not ##\bar\omega##?
vesta33
- 5
- 0
NascentOxygen and DrClaude, thank you for answers. I plotted this without elliptic integral. But this article referred to elliptic integrals. DrClaude, I am aware of your writings but mathematica has given error mesage:
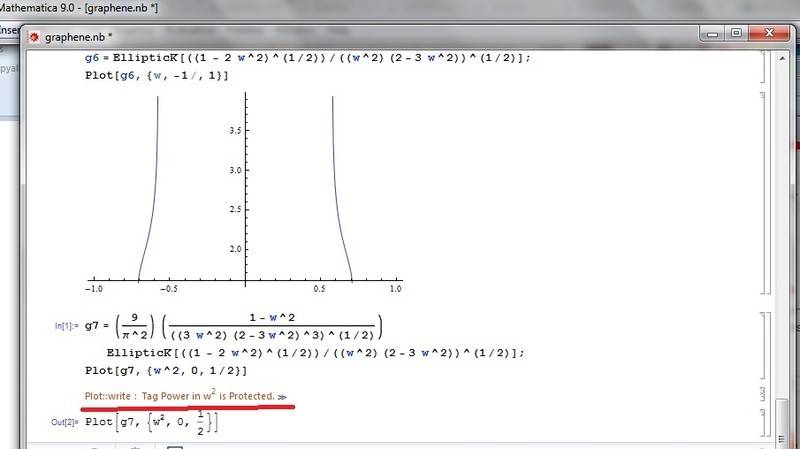
Last edited:
DrClaude
Mentor
- 8,477
- 5,693
Instead of using w^2 in the equation for g7, define a variable w2 that corresponds to ##\bar\omega^2##.
vesta33
- 5
- 0
I had tried.
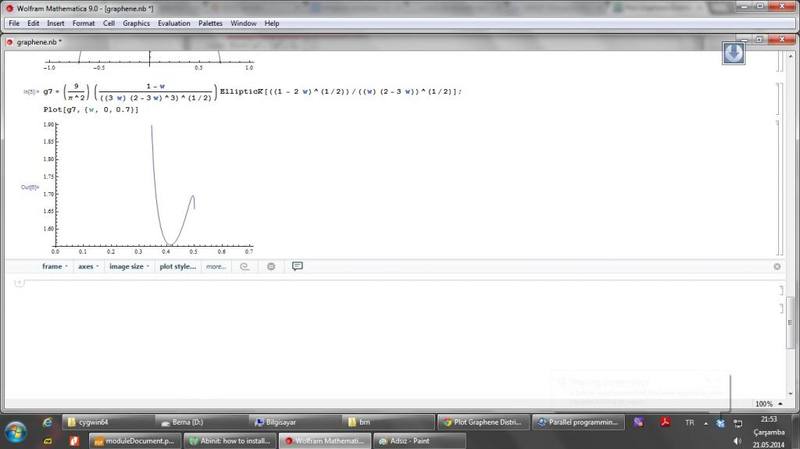
DrClaude
Mentor
- 8,477
- 5,693
In the argument of the elliptic integral, you're missing the cube in ##(2-3\bar\omega^2)^3##.
DrClaude
Mentor
- 8,477
- 5,693
You posted this in a homework forum, but am I correct in assuming that this is not homework?
Looking at your file, you have in it
First, the argument of the elliptic integral is incorrect. The square root should be over the argument itself, not the entire integral. Second, you need to plot with respect to w, not w^2. Third, the equation for g you have there is only valid in the range ##1/3 \leq \bar\omega^2 \leq 1/2##. Therefore, you should have
Looking at your file, you have in it
Code:
g2 = (9/\[Pi]^2) ((1 - 2 w)/(3 w (2 - 3 w)^3)^(1/2))
(EllipticK[(1 - 2 w)/(w (2 - 3 w)^3)])^(1/2);
Plot[g2, {w^2, 0, 1}]
Code:
g2 = (9/\[Pi]^2) ((1 - 2 w)/(3 w (2 - 3 w)^3)^(1/2))
EllipticK[((1 - 2 w)/(w (2 - 3 w)^3))^(1/2)];
Plot[g2, {w, 1/3, 1/2}]
vesta33
- 5
- 0
I should stress that I know mathematica. I had tried all possibly variaions before wrote here. If anyone wants help me please first of all run the code. I think mathematica or the article has a bug. Please nobody reply the message without running the code.
DrClaude
Mentor
- 8,477
- 5,693
I will try to be as diplomatic as possible, but your latest post has made me cross. I was guiding you towards the solution to your problem, but instead of trying what I suggested, you reply without any new attempts.
is not valid.
Then you should know why the statementvesta33 said:I should stress that I know mathematica.
Code:
Plot[g2, {w^2, 0, 1}]Obviously not, because you have not been able to reproduce the graph.vesta33 said:I had tried all possibly variaions before wrote here.
I did, told you what was wrong, and even gave you a correct replacement code, which is at least valid for part of the ##\bar{\omega}## domain.vesta33 said:If anyone wants help me please first of all run the code.
Both are fine. I was able to reproduce the figure in a couple of minutes. Before you ask for my code, note that this is not how things are done on PF. We don't feed you fish, we help with the fishing.vesta33 said:I think mathematica or the article has a bug.
Please do not reply before taking into account the replies of others.vesta33 said:Please nobody reply the message without running the code.
Similar threads
- Replies
- 6
- Views
- 2K
- Replies
- 18
- Views
- 3K
- Replies
- 6
- Views
- 2K
- Replies
- 15
- Views
- 2K
- Replies
- 5
- Views
- 2K
- Replies
- 15
- Views
- 2K
- Replies
- 7
- Views
- 2K
- Replies
- 15
- Views
- 2K
- Replies
- 1
- Views
- 2K
Hot Threads
-
Engineering Why is my output current so low in this Transconductance Amplifier cell?
- Started by arhzz
- Replies: 13
- Engineering and Comp Sci Homework Help
-
LTspice: Implementing a Single Balanced BJT Mixer
- Started by SumDood_
- Replies: 17
- Engineering and Comp Sci Homework Help
-
Max water pressure allowable on solar panels
- Started by ethanesh
- Replies: 16
- Engineering and Comp Sci Homework Help
-
Spiral scissor lift statics
- Started by carlcla
- Replies: 4
- Engineering and Comp Sci Homework Help
Recent Insights
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 7
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 0
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 91
- General Math
-
Insights Why Vector Spaces Explain The World: A Historical Perspective
- Started by fresh_42
- Replies: 0
- General Math