member 428835
Hi PF!
I'm plotting a line in TikZ using the following code
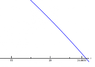
The largest zero is 24.0699 but latex is plotting that zero much larger. I've attached a picture so you can see what I'm referring to. Any ideas as to why this is happening?
I'm plotting a line in TikZ using the following code
Code:
\draw[domain=0:25,samples=100,color=blue,variable=\x,line width=1.5] plot (\x,{0.9924686128641765 - 0.023406305144575135*\x -
0.0006942621866861979*\x^2 - .000001925581045950128*\x^3});The largest zero is 24.0699 but latex is plotting that zero much larger. I've attached a picture so you can see what I'm referring to. Any ideas as to why this is happening?