patric44
- 308
- 40
hi guys
i was trying to came up with a basic code that could show me the band gaps in a solid after adding the periodic potential term to my solution :
$$ E = \frac{ħ^2q^2}{2m} \pm Vg $$
where Vg is my periodic potential , q is the k values in the first billion zone
from my understanding if i set the potential = 0 , i will get the normal parabolic dispersion for the free electron model , but once i introduce the potential it will create a separation at certain values of k which will indicate the forbidden gaps .
i tried to create that in python :
[CODE lang="python" title="the plot of energy values with a periodic potential function"]from scipy import signal
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.style
import matplotlib.colors
m = 1
ħ = 1
G = 50
K = 200
E1 = []
E2 = []
E3 = []
x1 = []
x2 = []
x3 = []
def energy1(q):
erg1 = ((ħ**2 * (q-G)**2 )/(8*m))+ np.cos(q)
return erg1
def energy2(q):
erg2 = ((ħ**2 * q**2 )/(8*m))+ np.cos(q)
return erg2
def energy3(q):
erg3 = ((ħ**2 * (q+G)**2 )/(8*m))+ np.cos(q)
return erg3
for z in range(-K,K):
x1.append(z)
E1.append(energy1(z))
for z in range(-K,K):
x2.append(z)
E2.append(energy2(z))
for z in range(-K,K):
x3.append(z)
E3.append(energy3(z))
plt.plot(x1,E1,'r')
plt.plot(x1,E2,'g')
plt.plot(x1,E3,'b')
plt.axvline(x=G)
plt.axvline(x=-G)
plt.grid()
plt.show()[/CODE]
and it gives that :
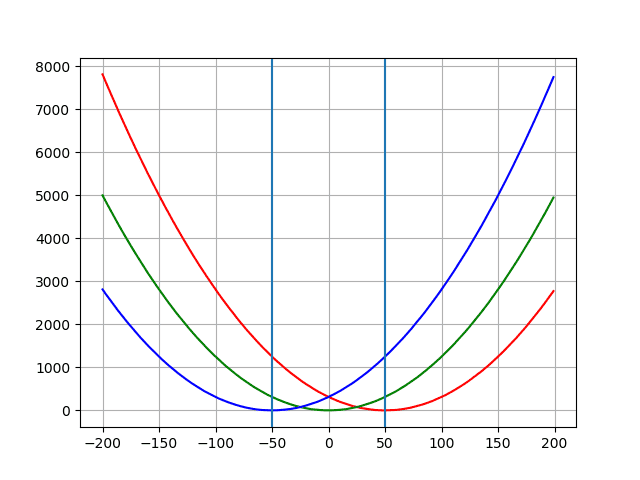
i was just trying to see the effect of basic periodic function like the sin , but there is no gaps! ,
i must be missing something or doing something wrong ?
any help will be appreciated , thanks
i was trying to came up with a basic code that could show me the band gaps in a solid after adding the periodic potential term to my solution :
$$ E = \frac{ħ^2q^2}{2m} \pm Vg $$
where Vg is my periodic potential , q is the k values in the first billion zone
from my understanding if i set the potential = 0 , i will get the normal parabolic dispersion for the free electron model , but once i introduce the potential it will create a separation at certain values of k which will indicate the forbidden gaps .
i tried to create that in python :
[CODE lang="python" title="the plot of energy values with a periodic potential function"]from scipy import signal
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.style
import matplotlib.colors
m = 1
ħ = 1
G = 50
K = 200
E1 = []
E2 = []
E3 = []
x1 = []
x2 = []
x3 = []
def energy1(q):
erg1 = ((ħ**2 * (q-G)**2 )/(8*m))+ np.cos(q)
return erg1
def energy2(q):
erg2 = ((ħ**2 * q**2 )/(8*m))+ np.cos(q)
return erg2
def energy3(q):
erg3 = ((ħ**2 * (q+G)**2 )/(8*m))+ np.cos(q)
return erg3
for z in range(-K,K):
x1.append(z)
E1.append(energy1(z))
for z in range(-K,K):
x2.append(z)
E2.append(energy2(z))
for z in range(-K,K):
x3.append(z)
E3.append(energy3(z))
plt.plot(x1,E1,'r')
plt.plot(x1,E2,'g')
plt.plot(x1,E3,'b')
plt.axvline(x=G)
plt.axvline(x=-G)
plt.grid()
plt.show()[/CODE]
and it gives that :
i was just trying to see the effect of basic periodic function like the sin , but there is no gaps! ,
i must be missing something or doing something wrong ?
any help will be appreciated , thanks