- #1
daudaudaudau
- 302
- 0
Hi. I'm trying to understand how the current in a PN junction depends on various parameters. I have found this formula in Ashcroft and Mermin. It looks like the current will increase if we decrease the density of donors and/or acceptors, Na and Nd. Is this correct?
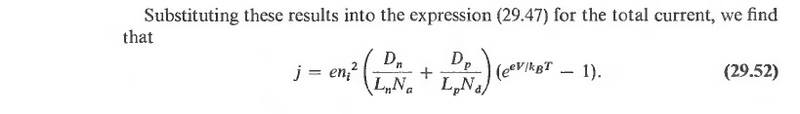
Last edited: