Point Triangulation in Fixed Space

[matsalleh]

Hello,

I'm an undergraduate electornics engineer.

I'm trying to design a system where I am able to find my relative position in a room. Using electronics, I am able to find the angles between the corners of the room, as observed from the point. I also know the dimensions of the room. Using this information I should logically be able to find my position.

I've been trying for the last 2 days to come up with an equation. However, everything I come up with is heavily linear dependant on each other; I'm going round in circles.

The picture below better explains my problem:

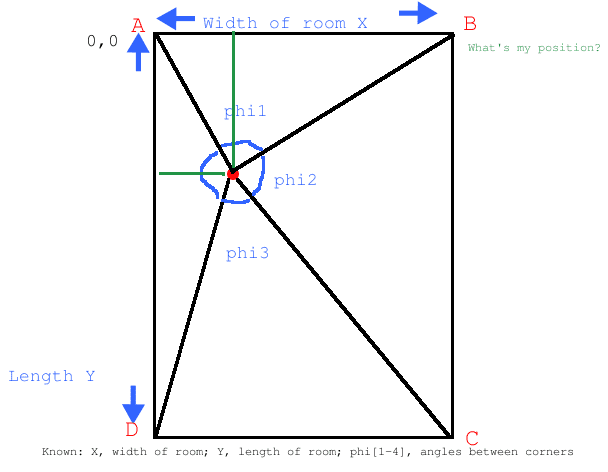
Has anyone any ideas on how I might find my relative position using the angles phi[1-4] and the dimensions of the room?

Thanks in advance,

Chris Adams.

 

[Studiot]

Hello, matsalleh.

The process you are describing is called resection, not triangulation.

You need at least three known points (you have 4) to provide a 'fix' as surveyors speak or 'mark' as navigators speak.

There are several methods of calculation available by searching the net.

 

[AlephZero]

I'm going round in circles.

That's a nice pun, because given one of your angle measurements, you know the point really does lie on the arc of a circle.

If you want to figure it out for yourself rather than just look up the answer, this might help:
http://www.mathsteacher.com.au/year10/ch06_geometry/09_angles_same_segment/segment.htm

 

[matsalleh]

Hello, matsalleh.

The process you are describing is called resection, not triangulation.

You need at least three known points (you have 4) to provide a 'fix' as surveyors speak or 'mark' as navigators speak.

There are several methods of calculation available by searching the net.

I googled it and came to this: http://www.map-reading.com/resect.php

I don't understand how this helps me? I need an analytical way of calculating my position, using a computer/micro-controller.

That's a nice pun, because given one of your angle measurements, you know the point really does lie on the arc of a circle.

If you want to figure it out for yourself rather than just look up the answer, this might help:
http://www.mathsteacher.com.au/year10/ch06_geometry/09_angles_same_segment/segment.htm

Haha, I had that idea just before I slept last night (sad I know). I didn't really know where to go with it?

Can you nudge me in the right direction?

Thanks,

Chris.

 

[Studiot]

I don't like to post weblinks here but this is what you need

http://www.engineeringsurveyor.com/images/resection.gif

 

[I like Serena]

Welcome to PF, matsalleh!Here's a different method.

You can set up a series of 4 equations for each angle as a function of x and y.

The 4 equations are:
$$\phi_1(x,y) = \arctan{x \over y} + \arctan{W - x \over y}$$
$$\phi_2(x,y) = \arctan{y \over W - x} + \arctan{L - y \over W - x}$$
$$\phi_3(x,y) = \arctan{x \over L - y} + \arctan{W - x \over L - y}$$
$$\phi_4(x,y) = \arctan{y \over x} + \arctan{L - y \over x}$$

Typically you would minimize the squared errors of the angles, assuming you can measure all 4 angles with equal precision.
That is, you would want to minimize the following function LSQ(x,y) by altering x and y:
$$LSQ(x,y) = (\phi_1 - \phi_1(x,y))^2 + (\phi_2 - \phi_2(x,y))^2 + (\phi_3 - \phi_3(x,y))^2 + (\phi_4 - \phi_4(x,y))^2$$
In this formula $\phi_1, \phi_2, \phi_3, \phi_4$ are the measured angles, and $\phi_1(x,y), \phi_2(x,y), \phi_3(x,y), \phi_4(x,y)$ are the formulas for the angles based on x and y.For a more accurate result you could use for instance the Levenberg-Marquardt algorithm to find an optimal solution.

 

[matsalleh]

I don't like to post weblinks here but this is what you need

http://www.engineeringsurveyor.com/images/resection.gif

I don't know angles A,B and C :(

Welcome to PF, matsalleh!


Here's a different method.

You can set up a series of 4 equations for each angle as a function of x and y.

The first 2 equations are:
$$\phi_1 = \pi - \arctan{y \over x} - \arctan{y \over W-x}$$
$$\phi_2 = \pi - \arctan{W - x \over y} - \arctan{W-x \over L - y}$$

You could solve these 2 equations numerically giving you x and y.

For a more accurate result you could set up all 4 equations and use for instance the Levenberg-Marquardt algorithm to find an optimal solution.
Typically you would minimize the squared errors of the angles, assuming you can measure all 4 angles with equal precision.
That is, you would minimize:
$$(\phi_1 - \phi_1(x,y))^2 + (\phi_2 - \phi_2(x,y))^2 + (\phi_3 - \phi_3(x,y))^2 + (\phi_4 - \phi_4(x,y))^2$$

It's been a few years since I've done maths like that. Alter x and y until phi[1-4] is satisfied?

I'd like to implement this solution with C, is there kind of optimised algorithm to do this? I didn't really understand the last bit of your post.

What about using arcs? I have a good feeling about using arcs.

Thanks,

Chris.

 

[I like Serena]

It's been a few years since I've done maths like that. Alter x and y until phi[1-4] is satisfied?

Yes.
With phi[1-4] the system is over determined, meaning you will not be able to find a perfect solution.
You can only minimize a predefined target function for which I suggest the sum of squares formula I gave (non-linear least squares method).

I'd like to implement this solution with C, is there kind of optimised algorithm to do this? I didn't really understand the last bit of your post.

What about using arcs? I have a good feeling about using arcs.

Thanks,

Chris.

In its simplest form you could start with an (x,y) in the middle of the room, take one step in each of the 4 directions and check in which direction the target function gets a lower value.
Then repeat until you cannot find such a direction any more.

There is a standard algorithm for problems like this, called the Levenberg-Marquardt algorithm:
http://en.wikipedia.org/wiki/Levenberg–Marquardt_algorithm

There are many implementations for it, which are referred to in the wikipedia article.
If you are programming in C you may be interested in the levmar implementation which is freely downloadable:
http://www.ics.forth.gr/~lourakis/levmar/

 

[AlephZero]

It should be fairly obvious that $\phi_1 + \phi_2 + \phi_3 + \phi_4 = 360$ degrees, so you really only have 3 measurements not 4.

The minimum amount of data is three points and two angles, but if you have three angles you can find the equations of the 3 circles (it's easy to find the center of each circle - see the website in my first link). Then you have 3 equations of the form

$x^2 + y^2 + a_1 x + b_1 y + c_1 = 0$
$x^2 + y^2 + a_2 x + b_2 y + c_2 = 0$
$x^2 + y^2 + a_3 x + b_3 y + c_3 = 0$

You can subtract them in pairs to get rid of the $x^2 + y^2$ terms, then you have two simultaneous linear equations to solve for x and y.

$(a_2 - a_1) x + (b_2 - b_1) y + (c_2 - c_1) = 0$
$(a_3 - a_1) x + (b_3 - b_1) y + (c_3 - c_1) = 0$

 

[I like Serena]

For reference I have edited post #6 with the proper equations.

Note that the formulas guarantee that the sum of the angles is 360 degrees.
It remains useful to measure the 4th angle to minimize the effects of measurement errors and to maximize the precision of the result.

 

[matsalleh]

It should be fairly obvious that $\phi_1 + \phi_2 + \phi_3 + \phi_4 = 360$ degrees, so you really only have 3 measurements not 4.

The minimum amount of data is three points and two angles, but if you have three angles you can find the equations of the 3 circles (it's easy to find the center of each circle - see the website in my first link). Then you have 3 equations of the form

$x^2 + y^2 + a_1 x + b_1 y + c_1 = 0$
$x^2 + y^2 + a_2 x + b_2 y + c_2 = 0$
$x^2 + y^2 + a_3 x + b_3 y + c_3 = 0$

You can subtract them in pairs to get rid of the $x^2 + y^2$ terms, then you have two simultaneous linear equations to solve for x and y.

$(a_2 - a_1) x + (b_2 - b_1) y + (c_2 - c_1) = 0$
$(a_3 - a_1) x + (b_3 - b_1) y + (c_3 - c_1) = 0$

What three circles? Would you be able to draw a diagram?

For reference I have edited post #6 with the proper equations.

Note that the formulas guarantee that the sum of the angles is 360 degrees.
It remains useful to measure the 4th angle to minimize the effects of measurement errors and to maximize the precision of the result.

That algorithm goes way beyond my understanding of mathematics.

And I really have no clue on how to use levmar. All the examples talk about curve fitting and stuff.

*straight over my head*

I get how you have derived derived the first 4 equations; simple trig.

However, I've never heard of this minimising square thing? (function LSQ) How is that derived?

Is there a systematic way in altering x and y to minimise the function LSQ?

Thanks,

Chris.

 

[I like Serena]

However, I've never heard of this minimising square thing? (function LSQ) How is that derived?

It is the method of the least squares:
http://en.wikipedia.org/wiki/Least_squares

Is there a systematic way in altering x and y to minimise the function LSQ?
Thanks,
Chris.

Here's a C code fragment (untested) that should do the trick without Levenberg-Marquardt.

This code will find your x and y coordinates with an accuracy of dx and dy that you can arbitrarily choose.

If a proper solution is found the function returns 0.
*pstdev_angle gives the average mismatch of the angles (as a standard deviation).
If it is too big, you have a misfit, which would occur if your angles are wrong.
*px and *py receive the solution for x and y.

If no solution was found, the function returns 1.

For this code to work, you need to implement another function LSQ(x,y) that calculates the formulas I gave.

int fit_angles(double W, double H, const double phi[4], double dx, double dy, double *px, double *py, double *pstdev_angle)
{
   double x = W/2;
   double y = H/2;
   double minsq = LSQ(x, y);
   double stepsq;
   int keepgoing = 1;

   while (keepgoing && (x >= 0) && (y >= 0) && (x <= W) && (y <= H))
   {
      keepgoing = 0;
      stepsq = LSQ(x+dx, y);
      if (stepsq < minsq)
      {
         minsq = stepsq;
         x += dx;
         keepgoing = 1;
      }
      stepsq = LSQ(x-dx, y);
      if (stepsq < minsq)
      {
         minsq = stepsq;
         x -= dx;
         keepgoing = 1;
      }
      stepsq = LSQ(x, y+dy);
      if (stepsq < minsq)
      {
         minsq = stepsq;
         y += dy;
         keepgoing = 1;
      }
      stepsq = LSQ(x, y-dy);
      if (stepsq < minsq)
      {
         minsq = lsq1;
         y -= dy;
         keepgoing = 1;
      }
   }

   *px = x;
   *py = y;
   *pstdev_angle = sqrt(minsq / 4);

   return keepgoing;
}

 

[Studiot]

I don't know angles A,B and C :(

I can't imagine why not, some are right angles in your case, since they are the angles at the corners of your room. The others can easily be obtained from the coordinates and are fixed for any room.

You should also look up the 'danger circle' since it is impossible to solve certain points within the room, with certain of the corners.

http://www.surveyequipment.com/PDFs/QuickGuide_TPS800_Resection.pdf

This is also the reason a cotangent formula was used not a tangent formula - to avoid division by zero.

 

[matsalleh]

It is the method of the least squares:
http://en.wikipedia.org/wiki/Least_squares




Here's a C code fragment (untested) that should do the trick without Levenberg-Marquardt.

This code will find your x and y coordinates with an accuracy of dx and dy that you can arbitrarily choose.

If a proper solution is found the function returns 0.
*pstdev_angle gives the average mismatch of the angles (as a standard deviation).
If it is too big, you have a misfit, which would occur if your angles are wrong.
*px and *py receive the solution for x and y.

If no solution was found, the function returns 1.

For this code to work, you need to implement another function LSQ(x,y) that calculates the formulas I gave.

int fit_angles(double W, double H, const double phi[4], double dx, double dy, double *px, double *py, double *pstdev_angle)
{
   double x = W/2;
   double y = H/2;
   double minsq = LSQ(x, y);
   double stepsq;
   int keepgoing = 1;

   while (keepgoing && (x >= 0) && (y >= 0) && (x <= W) && (y <= H))
   {
      keepgoing = 0;
      stepsq = LSQ(x+dx, y);
      if (stepsq < minsq)
      {
         minsq = stepsq;
         x += dx;
         keepgoing = 1;
      }
      stepsq = LSQ(x-dx, y);
      if (stepsq < minsq)
      {
         minsq = stepsq;
         x -= dx;
         keepgoing = 1;
      }
      stepsq = LSQ(x, y+dy);
      if (stepsq < minsq)
      {
         minsq = stepsq;
         y += dy;
         keepgoing = 1;
      }
      stepsq = LSQ(x, y-dy);
      if (stepsq < minsq)
      {
         minsq = lsq1;
         y -= dy;
         keepgoing = 1;
      }
   }

   *px = x;
   *py = y;
   *pstdev_angle = sqrt(minsq / 4);

   return keepgoing;
}

I actually designed a bit of code using 2 for loops before I saw your example. It's actually surprisingly quick:

#include <stdio.h>
#include <math.h>

#define STEP 1
#define THRESHOLD 0.0005
#define ANGLES 4

float lsq(int w, int l, float x, float y, float p[]);

int main(void){
	
	float W, L;
	
	float p[ANGLES];
	
	int i;
	
	float x, y;
	
	float test;
	
	printf("Room width:\n");
	scanf("%f", &W);
	printf("Room length:\n");
	scanf("%f", &L);
	
	for(i = 0; i <= (ANGLES - 1); ++i){
		printf("Angle %d:\n", (i+1));
		scanf("%f", &p[i]);
	}

	for(i = 0; i <= (ANGLES -1); ++i)
		p[i] = ((p[i]*M_PI)/180);
	
	for(x = 0; x <= W; x += STEP){
		for(y = 0; y <= L; y += STEP){
			printf("Trying x: %f and y: %f", x, y);
			printf("\r");
			test = lsq(W, L, x, y, p);
			if(test <= THRESHOLD)
				break;
		}
		if(test <= THRESHOLD)
			break;
	}
	
	printf("\n\nX is %f\n", x);
	printf("Y is %f", y);
	
	return 0;
}

float lsq(int W, int L, float x, float y, float p[]){

	float pTest[4];
	
	int i;
	
	float output = 0.0;
		
	pTest[0] = atan(x/y) + atan((W-x)/y);
	pTest[1] = atan(y/(W-x)) + atan((L-y)/(W-x));
	pTest[2] = atan(x/(L-y)) + atan((W-x)/(L-y));
	pTest[3] = atan(y/x) + atan((L-y)/x);
	
	for(i = 0; i <= (ANGLES - 1); ++i){
		output = (output + pow((p[i] - pTest[i]), 2.0));
	}
	
	return output;
	
}

My next question is, how do I calculate a good value for my threshold? (my LSQ)

• My device's angle measurement has a resolution of 1.8 degrees.
  
• My grid size is 1cm. My room size is up to 10 meter squared, but typically only around 5 sqm.

Also it's possible to minimise using only 2 angles. What gives the best results, using 2, 3 or 4 angles?

I can't imagine why not, some are right angles in your case, since they are the angles at the corners of your room. The others can easily be obtained from the coordinates and are fixed for any room.

You should also look up the 'danger circle' since it is impossible to solve certain points within the room, with certain of the corners.

http://www.surveyequipment.com/PDFs/QuickGuide_TPS800_Resection.pdf

This is also the reason a cotangent formula was used not a tangent formula - to avoid division by zero.

Ahh yeah I see now. I could, except I'd have a really big dead zone using only 3 corners...

I suppose I could algorithmically decide between corner C and D?

Thanks,

Chris.

 

[I like Serena]

I actually designed a bit of code using 2 for loops before I saw your example. It's actually surprisingly quick:

My next question is, how do I calculate a good value for my threshold? (my LSQ)

I recommend not using that threshold at all but to find the actual minimum.

It only speeds up your code by a factor of 2, but it loses accuracy unnecessarily and it gives your algorithm a preference for low x and y coordinates which is asymmetric.

• My device's angle measurement has a resolution of 1.8 degrees.
  
• My grid size is 1cm. My room size is up to 10 meter squared, but typically only around 5 sqm.

I would include an additional check that the resulting average mismatch of the angles is less than say $3 \times 1.8^\circ \approx 5^\circ$ to pick up on measurements that are totally wrong.

With a grid size of 1 cm and area 10 m² your algorithm needs $\propto 10^5$ iterations, which is just doable.

Note that the algorithm I gave needs $\propto 300$ iterations.

Also it's possible to minimise using only 2 angles. What gives the best results, using 2, 3 or 4 angles?

More measurements means better results with the additional bonus of being able to detect measurements that are totally wrong.

If you want to minimize on equipment 2 angles will suffice.
This should give you an accuracy of about 10 cm.

 

[Studiot]

Also it's possible to minimise using only 2 angles. What gives the best results, using 2, 3 or 4 angles?

With plenty of computing power available one simple way is to calculate all possibilities and take an average. This is much simpler than Least Squares and leads to a simpler answer.

Least Squares is not necessarily the best answer as some of the triangles in the fix will contain greater uncertainty than others and this varies with position. A weighting scheme helps, but where do you stop correcting it?

Another (surveyors) solution is to use three angles. In general this gives three position lines that enclose the real fix within a small triangle.
The real fix is then at the centroid of this triangle.

 

[I like Serena]

Least Squares is not necessarily the best answer as some of the triangles in the fix will contain greater uncertainty than others and this varies with position. A weighting scheme helps, but where do you stop correcting it?

That depends on the most significant source of measurement errors in the angles.
Is it a limitation of the device used to measure the angles?
Is it dictated by the distance to the corners?
Or is there some other dependency on position?

If it is the first, then the LSQ method I proposed gives the optimal result, since it assumes equal standard deviations in the measurement errors of the angles.

Otherwise a weighted LSQ could be used if you have more information on the accuracy of the angle measurements.
In my opinion, a (possibly weighted) LSQ gives the best results since it makes the best statistical fit.EDIT: Alternatively, you could create a lookup table.
You would have to calibrate that.
So you would measure the angles from a number of given positions and put those in a lookup table.
Then you could determine your position by simply looking up the closest entry, possibly interpolating with nearby entries.

 

[matsalleh]

I recommend not using that threshold at all but to find the actual minimum.

It only speeds up your code by a factor of 2, but it loses accuracy unnecessarily and it gives your algorithm a preference for low x and y coordinates which is asymmetric.




I would include an additional check that the resulting average mismatch of the angles is less than say $3 \times 1.8^\circ \approx 5^\circ$ to pick up on measurements that are totally wrong.

With a grid size of 1 cm and area 10 m² your algorithm needs $\propto 10^5$ iterations, which is just doable.

Note that the algorithm I gave needs $\propto 300$ iterations.




More measurements means better results with the additional bonus of being able to detect measurements that are totally wrong.

If you want to minimize on equipment 2 angles will suffice.
This should give you an accuracy of about 10 cm.

Can you just confirm how your algorithm works? It starts at half way and then tests each direction?

I don't see how it's possible to get zero without using a really really small step size (infinitely small) ?

And yes, it's a device limitation, the stepper motor I'm using only moves in 1.8degrees.

 

[I like Serena]

Can you just confirm how your algorithm works? It starts at half way and then tests each direction?

Yes.
You can compare it to the situation that you stand in the middle of a landscape with a valley.
To reach the lowest point you follow the path with the steepest descent.

I don't see how it's possible to get zero without using a really really small step size (infinitely small) ?

You won't get zero.

You will reach some minimum (greater than zero) while you're still at most dx or dy away from the best minimum (also greater than zero).
To get even closer to the real minimum you could reduce the step sizes dx and dy and retry.

So with a step size of 1 cm you get within 1 cm of the best position.
Closer is probably not useful for you, since you are limited to an accuracy of 1.8 degrees in your angles.

 

[matsalleh]

Yes.
You won't get zero.

You will reach some minimum (greater than zero) while you're still at most dx or dy away from the best minimum (also greater than zero).
To get even closer to the real minimum you could reduce the step sizes dx and dy and retry.

So with a step size of 1 cm you get within 1 cm of the best position.
Closer is probably not useful for you, since you are limited to an accuracy of 1.8 degrees in your angles.

Okay, so my question is: If I can't get zero, what's my threshold for minimum?

Are you suggesting also, that I gradually decrease my step size until a solution is found?

So try with dx=1, no solution found, try dx = 0.1, no solution found, ...

??

Thanks,

Chris

 

[I like Serena]

Okay, so my question is: If I can't get zero, what's my threshold for minimum?

Are you suggesting also, that I gradually decrease my step size until a solution is found?

So try with dx=1, no solution found, try dx = 0.1, no solution found, ...

??

Thanks,

Chris

I suggest to use step sizes dx=1cm and dy=1cm.
If a solution is found within the bounds of your room, check if it is reasonable.

You can do this by calculating sqrt(LSQ(x,y) / NR_ANGLES) and check if it is less than ~5 degrees (converted to radians, so 5*M_PI/180).

 

[matsalleh]

I suggest to use step sizes dx=1cm and dy=1cm.
If a solution is found within the bounds of your room, check if it is reasonable.

You can do this by calculating sqrt(LSQ(x,y) / NR_ANGLES) and check if it is less than ~5 degrees (converted to radians, so 5*M_PI/180).

I don't understand you. If the device is @ 100.5,100.5; the algorithm will never find a solution with a step size of 1, surely I need to set the minimum to something slightly higher than zero?

What do you mean by, checking if it's reasonable?

Thanks,

Chris.

 

[I like Serena]

I don't understand you. If the device is @ 100.5,100.5; the algorithm will never find a solution with a step size of 1, surely I need to set the minimum to something slightly higher than zero?

Well, I do not understand you...
What do you mean by setting the minimum higher than zero?
The algorithm does not set the minimum to zero or anything like that.

The algorithm starts at an initial position in the middle, and keeps making steps of 1cm until it cannot find a better solution anymore.

What do you mean by, checking if it's reasonable?

Thanks,

Chris.

Suppose you measure 4 angles that for some reason add up to 400 degrees.
This should not be possible, since they should add up to approximately 360 degrees, so at least one angle must have a wrong measurement.

The algorithm will still find a solution that fits best with the data.
However, if you calculate the corresponding angles, they would typically be more than 5 degrees off.
From this you can conclude that you have a wrong measurement and the solution will be way off (from the principle: garbage in - garbage out).

 

[Studiot]

That depends on the most significant source of measurement errors in the angles.

Hello, ILS - It is not often you and I disagree, but have you considered the effect of receiving angle or angle of cut of the intersecting loci of points with a given receiving angle?

Say, for instance the roving point (P) was 1mm from edge AB and both A and B were used as known fixed points. Angle APB would be almost 180, leading to a very poor solution.

 

[matsalleh]

Well, I do not understand you...
The algorithm starts at an initial position in the middle, and keeps making steps of 1cm until it cannot find a better solution anymore.

Ahhhh now I get you! I thought we were testing for zero!

Suppose you measure 4 angles that for some reason add up to 400 degrees.
This should not be possible, since they should add up to approximately 360 degrees, so at least one angle must have a wrong measurement.

The algorithm will still find a solution that fits best with the data.
However, if you calculate the corresponding angles, they would typically be more than 5 degrees off.
From this you can conclude that you have a wrong measurement and the solution will be way off (from the principle: garbage in - garbage out).

Why don't I just check they add up to 360, then take some kind of average or something?

Or maybe we just use 3 angles?

Thanks,

(I really mean it, you've helped me a lot!)

Do you want me to credit you in my paper? :D

Chris

 

[I like Serena]

Hello, ILS - It is not often you and I disagree, but have you considered the effect of receiving angle or angle of cut of the intersecting loci of points with a given receiving angle?

Say, for instance the roving point (P) was 1mm from edge AB and both A and B were used as known fixed points. Angle APB would be almost 180, leading to a very poor solution.

Hi Studiot!

Perhaps there is some confusion about which LSQ is calculated exactly?
With an LSQ of the position-mismatch you would be right and LSQ would be bad.

But it is not the position-mismatch of which the LSQ is calculated, but the angle-mismatch.
That way one angle (angle of cut) can give a greater contribution to the position than a second angle.However, I have to admit that the type of measurement error matters.
I am making the assumption that the angle measurement errors are normally distributed and independent of each other.

Since it is a stepping motor, that suggests it is discretely distributed.
And if the measurements are connected somehow, they may not be independent from each other.
In these cases LSQ may give an inferior fit.
In such cases your solution would be better, charting which angle you get where.
To overcome discrete measurement problems, you would need to be able to say which discrete value of the angle goes where though...

Ahhhh now I get you! I thought we were testing for zero!

:)

Why don't I just check they add up to 360, then take some kind of average or something?

Or maybe we just use 3 angles?

The algorithm itself already takes a kind of average so there is no need to compensate in another way.
The problem is that you would not know which angle is bad.
But if you use an angle that is bad, the result will be way off.

Thanks,

(I really mean it, you've helped me a lot!)

Do you want me to credit you in my paper? :D

Chris

Can you, can you?!