Poisson distribution on a simulated (SSA) data set

[tolove]

I've been asked to fit the histogram with a Poisson distribution as part of a mostly independent learning thing. The data was produced through a stochastic simulation.

Can someone get me started on how I would go about finding the expected distribution?

If you need additional information, or if you would like to see the code (python), please ask.

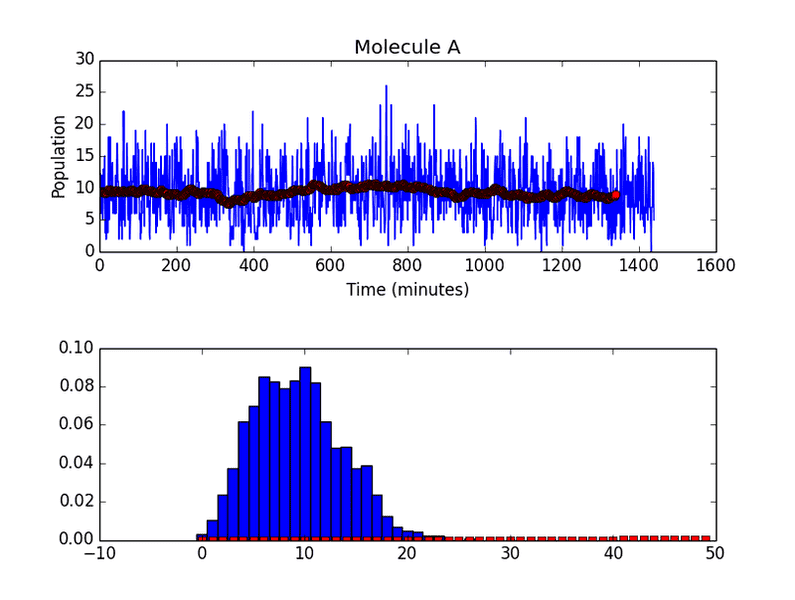
Thanks for your time!

 

[bpet]

If your data is coming from time-series observations, then perhaps a more important question is *should* you be fitting the data directly to a distribution?

 

[tolove]

If your data is coming from time-series observations, then perhaps a more important question is *should* you be fitting the data directly to a distribution?

That's what I'm thinking, but I was specifically asked to set a Poisson distribution to this. So there must be a way that the propensities can be used to find a prediction. Or at least a close approximation for long times.

I don't know how to go about this, though.

 

[FactChecker]

That's what I'm thinking, but I was specifically asked to set a Poisson distribution to this. So there must be a way that the propensities can be used to find a prediction. Or at least a close approximation for long times.

I don't know how to go about this, though.

The mean of the sample approximates the λ parameter of the Poisson distribution. That defines the Poisson distribution. My guess is λ ~ 8.