Positive Ion passing through a Magnetic Field

[Electro n00b]

1.Homework Statement

BACKGROUND:
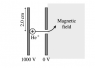
A positive helium ion He+ (mass 6.7 x 10-27 kg, charge 2e) is released from rest from the surface of a +1000 V electrode, as shown in the diagram below. It crosses (in vacuum) the gap between the electrodes, passes through a small hole in a 0 V electrode and into a magnetic field, and then begins to move in a curved path as shown. The magnetic field is uniform in the hatched region to the right of the 0 V electrode and is zero to the left of the 0 V electrode (Note: the lines do not indicate the direction of the magnetic field). The electrodes are circular disks with radius r = 2.0 cm and are separated by a distance d = 2.0 mm. The magnetic-field strength is 1.0 T. Picture attached of magnetic field and electrodes.

QUESTIONS:
(i) What is the direction of the magnetic field? Sketch the trajectory that the ion executes while it is within the magnetic field, and explain why the trajectory takes this shape.
(ii) Calculate the speed with which the ion enters the magnetic field, and use this to determine whether the ion can exit the magnetic field without colliding with the 0 V electrode.
(iii) Explain qualitatively how your answer to (ii) would change if the potential difference across the electrodes were increased.

2. Homework Equations
Part i)right hand rule?
Part ii) qU = 1/2 mv^2 , U being the voltage



3. The Attempt at a Solution

For part i) When I use the right hand rule on this question I get that the magnetic field would be coming out of the page but I'm not overly confident that I am correct. The trajectory would be looping back on the 0V electrode in a counter clockwise direction.

Part ii) I used the qU = 1/2 mv^2 formula to get v = √((2qU)/m), which gave me 7.73 x 10^14 m/s
I'm not sure what equation to use to figure out if the ion can exit the magnetic field without colliding with the 0V electrode.

Part iii) As voltage is increase the velocity would increase due to voltage being on the numerator of the rearranged equation for part ii)

 

[Simon Bridge]

p1. Recheck your right-hand rule ... how did you use it? (I use a left-hand rule myself.)

p2. What is the shape of the trajectory that the charge will follow? What is the important parameter for that shape? What does that parameter have to be for the particle to miss the 0V plate?

In general, it is unusual for the solution to be a matter of locating the right equation and plugging numbers in.

 

[Electro n00b]

For p1 I understand that there is a relationship between magnetic field, velocity and magnetic force. F = qv x B.

So having a second look at this section I would change my answer to going into the page since velocity vector is pointing to the right and magnetic force appears to be pointing in towards the electrode.

For p2 the important parameter would be the radius of the circle and so I have to find a velocity that will make the radius of the ion's path be greater than the 2cm electrode?

Thanks for your help Simon :)

 

[Simon Bridge]

And - it's a positive charge ... the deflection you had was correct for a negative charge.
You remember your circular motion right? Everything is related.

Well done :)

 

[megt]

hey, I am working on the same problem at the moment, and i was just wondering what answer you ended up getting for the velocity as it entered the magnetic field?
I worked out that v=√((2*2000eV)/(6.7*10^-27)) = 309277m/s (note that I converted the eV to J before calculating.
Thanks

 

[Simon Bridge]

I converted the eV to J before calculating.

... I'll show you a trick:

1eV is the kinetic energy of an electron that has been accelerated through a potential difference of 1V.

For an electron: m_ec² = 511eV² (by E=mc².)

I can rewrite the equation for kinetic energy to use this:
K= \frac{1}{2}mv^2 = \frac{1}{2}(mc^2)\frac{v^2}{c^2}

So if you have kinetic energy in eV, the speed in m/s is $$v=(3\times 10^8)\sqrt{\frac{2K}{511}}$$... now aren't these much easier numbers to handle?
(This is for an electron - you can look it up for Helium (is that He⁺ or He²⁺?)

However - notice that electron00b's speed is faster than light?!

If the speed is going to be relativistic then the kinetic energy needs to be $$K=(\gamma -1) m_ec^2$$