wgas
- 3
- 0
in a microscopy class:
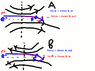
problem is to illustrate the path of a positron on both sides of the axis in a coil produced magnetic field. consider both cases of the particle's velocity and the magnetic field being a)in the same direction & b)in opposite directions.
i have no clue. any help? would it just be the opposite of an electron's path?
problem is to illustrate the path of a positron on both sides of the axis in a coil produced magnetic field. consider both cases of the particle's velocity and the magnetic field being a)in the same direction & b)in opposite directions.
i have no clue. any help? would it just be the opposite of an electron's path?
Last edited: