john-b
- 5
- 0
Homework Statement
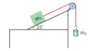
In the diagram, m1 has a mass of 47 kg and m2 has a mass of 35 kg. The coefficients of friction between m1 and the surface of the inclined plane are µs = 0.42 and µk = 0.19.
(a) If the masses are held in place and then released, will they start to move?
(b) If the answer to (a) is yes, what will be the acceleration of the masses?
(c) If the answer to (a) is no, how much mass would you have to add to m2 to cause the masses to begin to move?
(d) If the answer to (a) was no and you added the mass that you calculated in (c), what would be the acceleration of the masses?
Homework Equations
Fn = m x g x cosθ
Ff = μ x Fn
T = m x g
Mgx = m x g x sinθ
A = ΣF/m
The Attempt at a Solution
A = (35kg x 9.8 m/s^2) - (0.42 x 47 kg x 9.8 m/s^2 x cos(25)) - (47 kg x 9.8 m/s2 sin(25) / 82 kg = -0.32 m/s^2
I can't figure out what's wrong with my calculation because the book's answer to part a) is that there won't be any acceleration.
Help would be much appreciated. Thank you.