Frequently Made Errors in Mechanics – Friction

 

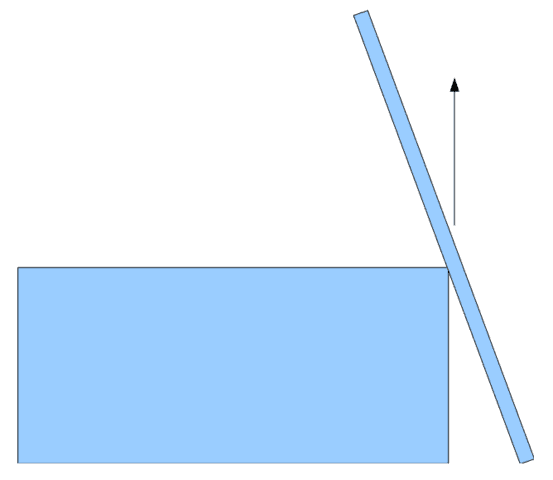
1. Direction of the normal

Definition: The normal force that body A exerts on body B is that force of minimum magnitude which suffices to prevent penetration of its surface.

X “the normal is at right angles to the horizontal”

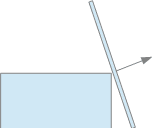
This mistake tends to arise when one of the bodies presents a sharp corner at the contact point, e.g. a rod leaning against an upper corner of a block.
✓ The normal is at right angles to the contact plane

 A general definition of contact plane is not straightforward.

• If either surface is differentiable at the point of contact it has a tangent plane there.
• If both surfaces have tangent planes at the contact point then they are necessarily the same plane, or the bodies would intersect.
• If only one has a tangent plane (as in the picture), use that.
• If neither has a tangent plane there, the direction of the normal is indeterminate.

 2. Direction of the frictional force

X “Friction opposes motion”

If a car is going at a steady pace uphill, the friction between the tyre of a driving wheel and the road is in the direction of motion, not against it. Otherwise, the car would not get up the hill! Without friction, the wheels would spin. The part of the tyre in contact with the ground would move down the slope, relative to the ground. Friction opposes this relative motion, so acts up the slope on the tyre.

For non-driving wheels, friction between tyre and road nearly always opposes the motion of the vehicle.  However, this friction is typically much less: it is only the frictional force required to provide angular acceleration to the wheel (to maintain rolling contact) and to overcome axial friction.

Even then, it can go the other way.  If a car is decelerating but not by braking of the non-driving wheel, the angular momentum of the wheel acts to maintain speed, and the frictional force will act on the car in the direction of motion.

Despite the complexities, all of these circumstances are encompassed by:

✓ The frictional force between two surfaces in contact opposes relative motion of the two surfaces.

3. Static frictional force

3.1 Magnitude

X “The magnitude of the force of static friction equals the static coefficient times the magnitude of the normal force, $|F_s| = \mu_s |F_N|$”

In static friction, μ_sN is merely the maximum value of the frictional force. The actual frictional force can be less.

✓ “The magnitude of the force of static friction is at most the static coefficient times the magnitude of the normal force, $|F_s| \leq \mu_s |F_N|$”

3.2 To slip or not to slip?

Some students become confused about when to use the static friction coefficient and when kinetic, particularly when motion is involved anyway.

Example 1: “A car travels around a circle radius R at a constant speed v. The static friction coefficient is $\mu_s$ and the kinetic friction coefficient is $\mu_k$. What is the maximum speed to avoid skidding?”

Attempted answer:
X “Since the car is moving we should use kinetic friction.  To avoid skidding $\frac {v^2}r \leq g\mu_k$.”

As long as the car is not skidding, the tyres are in rolling contact with the ground, so friction is static:

✓ $\frac {v^2}r \leq g\mu_s$.

Example 2: “Suppose the driver decides the speed is too great for the curve and brakes slightly part the way round.  What is the maximum safe deceleration?”

Attempted answer:

X “The maximum deceleration force is $mg\mu_s$, so the maximum deceleration is $g\mu_s$.”

The total frictional force is a vector, and its magnitude cannot exceed $mg\mu_s$.  The centripetal acceleration and the tangential acceleration a are perpendicular, so the frictional force needed has magnitude $m\sqrt{\left(\frac{v^2}r\right)^2+a^2}$.  Hence

✓ $a^2 \leq (g\mu_s)^2-\left(\frac{v^2}r\right)^2$.

Example 3: “A block rests on an inclined plane which is gradually tilted until the block slips.  The static friction coefficient is $\mu_s$ and the kinetic friction coefficient is $\mu_k$.  What is the acceleration of the block?”

Attempted answer:

Since the block is slipping we should use kinetic friction coefficient. If the plane is at angle $\theta$ the normal force is $mg\cos(\theta)$.

X Since it is only just slipping, the frictional force is equal to the downplane gravitational force:

$mg\cos(\theta)\mu_k = mg\sin(\theta)$.

This will lead to the conclusion that the block does not accelerate!

The angle of the plane was determined by the limit of static friction:

✓ $mg\cos(\theta)\mu_s = mg\sin(\theta)$.

The net downplane force when slipping is therefore

$mg\cos(\theta)\mu_s-mg\cos(\theta)\mu_k$,

producing an acceleration

$g\cos(\theta)(\mu_s-\mu_k)=g(1+\mu_s^2)^{-\frac 12}(\mu_s-\mu_k)$.

Tip: If you sometimes mix up sine and cosine in inclined plane problems, think about the $\theta = 0$ case.  The normal force would be $mg$, and $\cos(0)=1$, so it must be $mg\cos(\theta)$.

 3.3 Range of possibilities for Static Frictional Force

In some questions, it might not be immediately apparent which way static friction will act.

“A car negotiates a bend radius R at speed v.  The road surface is banked at angle $\theta$, the lower side being on the inside of the bend, but level in the direction of travel.  Coefficient of static friction is $\mu_s$.  Under what condition on these variables will the car skid?”

Attempted answer:

Let the Normal force be N and the frictional force be F. 

Vertically, $N\sin(\theta)-F \cos(\theta)=mg$

Horizontally, $N\cos(\theta)+ F\sin(\theta)= m\frac{v^2}r$

X where to avoid skidding $0 \le F\le N\mu_s$

That solution assumes the car is in danger of sliding up the bank.  But on a steep bank at low speed, the risk might be sliding down it:

✓ where to avoid skidding $|F|\le N\mu_s$

3.4 Alternating kinetic friction

“A block mass … on a horizontal floor is attached to a wall via a spring constant ….  The coefficients of friction between block and floor are ….  The spring is extended distance … and the block released.  At what spring extension (or compression) does the block come to rest?”

This is quite tricky because not only might the kinetic friction keep reversing, but at each reversal it is possible that static friction will take hold.

3.5 Indeterminate frictional force

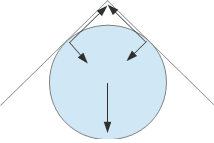
Situations can arise in which some static frictional forces cannot be determined.  This often occurs in ‘wedging’.

Example: A ceiling slopes down at 45 degrees each side of its apex.  A ball weight W is pushed into the apex.  The coefficient of static friction, $\mu_s$, is sufficient that the ball stays put.

$W+N\sqrt 2 = F\sqrt 2$

$F \leq \mu_s N$

So $W\leq N\sqrt 2 (\mu_s-1)$

The set-up can be stable as long as $\mu_s$ > 1.  Even if this coefficient is known, F and N cannot be determined exactly, but we can set lower bounds:

$N \geq \frac W{\sqrt 2 (\mu_s-1)}$

$F \geq \frac {W\mu_s}{\sqrt 2 (\mu_s-1)}$

4. Friction when Rolling

X “Rolling contact requires friction”

If a wheel is rolling at a steady speed on a level surface, no friction is required to maintain rolling.  Rolling just means the rotation matches the linear velocity in the relationship $\vec v = \vec{\omega}\times\vec r$.  If no forces are required to maintain the rotation and the velocity then no forces are required to maintain rolling.

X “Friction is required to initiate rolling”

While this is almost always true in practice, it isn’t strictly necessary. A wheel could be brought to exactly the right rotation rate for its forward motion before contacting the surface.

4.1  Friction versus Rolling Resistance

In the real world, a wheel rolling on level ground does slow down.  This is referred to as Rolling Resistance, but what is it?

Rolling resistance arises because all bodies are, to some extent, imperfectly elastic.  When compressed, the reaction force for a given extent of compression is greater during the compression phase than during the relaxation phase.  You get less work back out than you put in.

For a wheel rolling on a level floor, both the wheel and the floor are imperfectly elastic.  These two aspects of rolling resistance slow the motion in rather different ways.

If we take the floor as rigid but the wheel as elastic, the normal force is still vertical. Because the wheel deforms, instead of a point contact we have an area of contact.  In the front half of that area, compression is increasing, while in the rear half it is decreasing.  Because of the imperfect elasticity, the normal force is stronger in the front half than in the rear.  This leads to a torque opposing rotation.

If the wheel were to rotate more slowly, it would slide against the ground, therefore static friction arises.  This frictional force points backwards, thereby both slowing the linear motion of the wheel and maintaining rotation rate enough to keep rolling contact.

If we take the wheel as rigid but the floor as springy, the wheel is always sitting in a dip.  Again, the normal force (which points in different directions in different parts of the contact area now) is stronger in the front half than in the back.  This leads to a net normal force which is not vertical but points somewhat backwards relative to the motion.  To the wheel, it is as though it is going uphill.  That slows the forward motion of the wheel but does not apply a torque.  This time the frictional force points forwards, maintaining rolling contact by slowing the rotation and reducing the linear deceleration.

“A car mass m is moving on hard level ground at a constant speed v. A following wind of the same speed ensures there is no air resistance. The power output the engine is P. What is the frictional force between the road and the tyres?”

Attempted answer:

“Power = force*speed

X ∴ Frictional force = P/v”

Since there is no air resistance and the road is rigid and level, the only possible horizontal force on the car would be friction between road and tyres. If that is nonzero, the car must accelerate or decelerate.  It follows that there is no frictional force, so no work is being done against friction between tyre and road. So… why would any power be needed when driving at constant speed? There are several possibilities:

• As tyres roll, they deform. As each part comes into contact with the road it flattens. This constant flexing of the tyres takes energy, ending up as heat.
• There will also be friction in the axles etc.
• And of course, if the road is not level, then a force is also needed to oppose gravity

✓ Rolling resistance + air resistance + bearing friction + component of gravity along slope + braking force = P/v

 5. Work done by Friction

Some confusion may arise, particularly in language translation, between work done by and work done on.  If A does work W on B then the work done by A is W and the work done by B is -W.

“A drive belt rotates a wheel at constant angular speed, without slipping, against a resistive torque $\tau$.  How much work does friction between the belt and the wheel do in rotating it through an angle $\theta$?”

Attempted answer:

X “Since there is no relative movement between the surfaces in contact, the static frictional force does no work.”

Well, clearly something has done work $\tau\theta$ on the wheel, and the frictional force is the only candidate.

The trouble is that work can depend on the reference frame.

This Wikipedia entry is a bit confusing: http://en.wikipedia.org/wiki/Friction#Work_of_friction:

In the reference frame of the interface between two surfaces, static friction does no work, because there is never displacement between the surfaces. In the same reference frame, kinetic friction is always in the direction opposite the motion, and does negative work. However, friction can do positive work in certain frames of reference. One can see this by placing a heavy box on a rug, then pulling on the rug quickly. In this case, the box slides backwards relative to the rug, but moves forward relative to the frame of reference in which the floor is stationary. Thus, the kinetic friction between the box and rug accelerates the box in the same direction that the box moves, doing positive work.

If the two surfaces are in relative motion, what is the “reference frame of the interface“?

[There are different ways of conceptualising frictional losses.  In what follows, they are viewed as work done on the interface itself.]

Suppose the rug advances distance $x_r$ and exerts a frictional force $F$.  At the same time, the box slides a distance $x_b < x_r$ relative to the rug in the opposite direction.

In the ground frame, the box has advanced $x_r-x_b$, so the work done on it is $(x_r-x_b)F$ (that is, its frictional force has done work $(x_b-x_r)F$).  In the same frame, the rug has advanced $x_r$ and the frictional force it supplies has done work $x_rF$.  Work done by the interface is $-x_bF$.  Thus total work change = $(x_b-x_r)F+x_rF-x_bF = 0$.

In the reference frame of the rug, the force it exerts has not moved, so it did no work.  The force exerted by the box has advanced by $x_b$ in its direction, doing work $x_bF$, matching the work $-x_bF$ done by the interface.

In the reference frame of the box, the force it exerts has not moved, so it did no work.  The force exerted by the rug has advanced by $x_b$ in its direction, doing work $x_bF$, matching the work $-x_bF$ done by the interface.

To complete the picture, consider the rug-pulling example with static friction in the ground frame.  The static frictional force from the rug does work $x_rF$ and that from the box does work $-x_rF$.