. Arctic.
- 13
- 0
Homework Statement
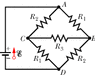
In the figure ε = 15.1 V, R1 = 1560 Ω, R2 = 2130 Ω, and R3 = 4210 Ω. What are the potential differences (in V) (a) VA - VB, (b) VB - VC, (c) VC - VD, and (d) VA - VC? The figure consists of single ideal batter connecting to a diamond shape circuit ABCD. Going clockwise starting with point A, line AB has resistor 1, line AD has resistor 2, line CD also has a resistor 1, and line CA also has a resistor two. A line between CB is between points C and B, and it contains resistor 3.
ε = 12V, R1 = 2000Ω, R2 = 3000Ω, R3 = 4000Ω
Homework Equations
ε - i1R2 - i2R2 = 0 (1)
ε - (i1 - i2)R3 = 0 (2)
The Attempt at a Solution
What I did was move around equation (2), so that I would end up with
i2 = i1 - (ε/R3), and then I would plug that back into equation one, which would help me find the current. The thing is that it doesn't match up with the answers in the book, so I would like to know how to reach the correct answer. i 1-3, in that order, are 0.002625 A, 0.00225 A, and 0.000375 A. Help would be much appreciated. Thanks.
Attachments
Last edited: