HWGXX7
- 46
- 0
Hello,
I have this problem with deriving the formule from de definition of potential energy
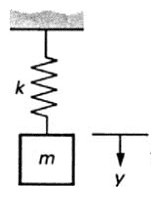
Picture show a mass-spring system in rest position:
In general potential energy can be written as dot product: \frac{dE_{P}}{d\overrightarrow{y}}=-\overrightarrow{F}.
Potential energy wil rise if, y rises. Because the direction of F is always inverse of y, this is correct.
But when the mass wil move upward trough it's equilibrium the potential energy will also rises, while y will decline. The derivative is negative, so the formule potential energy doesn't count anaymore.
How to fix this problem?
Also if you can look to my derivation of potential energy:
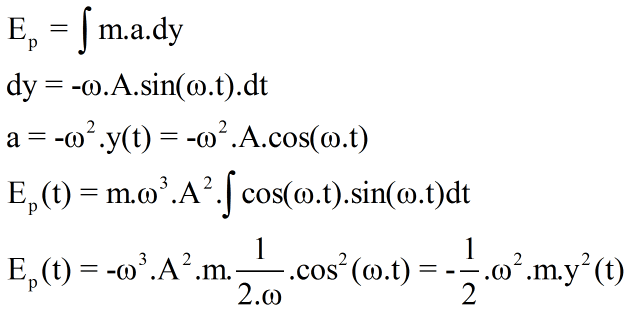
ty&grtz
I have this problem with deriving the formule from de definition of potential energy
Picture show a mass-spring system in rest position:
In general potential energy can be written as dot product: \frac{dE_{P}}{d\overrightarrow{y}}=-\overrightarrow{F}.
Potential energy wil rise if, y rises. Because the direction of F is always inverse of y, this is correct.
But when the mass wil move upward trough it's equilibrium the potential energy will also rises, while y will decline. The derivative is negative, so the formule potential energy doesn't count anaymore.
How to fix this problem?
Also if you can look to my derivation of potential energy:
ty&grtz
