- #1
amcavoy
- 665
- 0
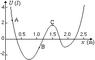
Basically, an object moves along a straight line (starting at rest) and reaches a maximum kinetic energy at .7 m. At 0 meters, the potential energy is 4 J and at .7 meters, the potential energy is -2 J. What is the maximum kinetic energy?
I know that the answer is 4 J. However, it would seem to me that the change in kinetic energy is equal to the negative potential energy.
[tex]\Delta K=K_f-K_i=K_f[/tex]
[tex]-U=\Delta K=2[/tex]
This seems that the kinetic energy is 2. Where am I going wrong?
Thanks for the help.
I know that the answer is 4 J. However, it would seem to me that the change in kinetic energy is equal to the negative potential energy.
[tex]\Delta K=K_f-K_i=K_f[/tex]
[tex]-U=\Delta K=2[/tex]
This seems that the kinetic energy is 2. Where am I going wrong?
Thanks for the help.