Power Calculation of general electric circuit

[PhysicsTest]

TL;DR

I want to calculate the power of general circuit with voltage leading the current by phase difference of Theta

I am trying to calculate the power calculation of a general circuit with voltage leading the current by a phase difference of $\theta$.
The instantaneous voltage is given by $v = V_m\sin(\omega t +\theta) ; i = I_m\sin(\omega t)$. The instantaneous power is then
$p = V_m I_m \sin(\omega t + \theta) * \sin(\omega t)$ ---> 1. The first doubt is if i draw the waveform

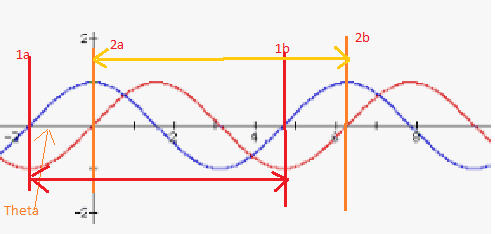
The average power is the power calculated for one cycle $P_{avg} = \frac {P_{1cycle}} {Duration of 1 Cycle}$ where $P_{1cycle}$ is the power for one cycle of the signal. Is my understanding correct? The duration of 1Cycle is $2\pi$?
2. The 1 cycle can be either from 0 to 2$\pi$ represented by 2a to 2b and hence the limits of integration are 0 to 2$\pi$ or it can be from 1a to 1b i.e the limits of integration from $-\theta$ to $2\pi - \theta$?
3. The integral will be
$\int_0^{2\pi} p d\theta$ or $\int_0^{2\pi} p dt$ ? How do i know which one to use? (p is from eq1)

 

[anorlunda]

You are on the right track. I would integrate with respect to time.

But I don't understand

The instantaneous power is then
p=VmImsin⁡(ωt+θ)∗sin⁡(ωt) ---> 1.

What do you mean by ---> 1?

See the Insights article
https://www.physicsforums.com/insights/ac-power-analysis-part-1-basics/

 

[PhysicsTest]

It means equation 1.

 

[PhysicsTest]

The derivation is
$\int_0^{2\pi} V_mI_m\sin(\omega t + \theta)*sin(\omega t) dt$
$\int_0^{2\pi} V_m I_m [\sin(\omega t) \cos(\theta) + \cos(\omega t) \sin(\theta)] \sin(\omega t) dt$
$\int_0^{2\pi} V_m I_m[\sin^2(\omega t) \cos(\theta) dt + \cos(\omega t) \sin(\omega t) \sin(\theta) dt]$
$P_{avg} = \frac{V_m I_m \pi \cos\theta} {2\pi} = \frac{V_mI_m\cos\theta} 2$
It does seem to match for resistor R $\theta = 0 ; P_{avg} = V_{rms}I_{rms}$
for pure inductor or capacitor $\theta = 90; P_{avg} = 0$

 

[maxwells_demon]

You actually have two options:

1) express ωt as an angle (let's say φ), and integrate wrt φ, with limits 0 to 2π or
2) express θ in seconds, and integrate wrt t, with limits 0 to 1/period (which would be (2π/ω))

both would give you the same average power value over 1 period, though you may want to stick with angles for the x-axis, assuming you want to arrive at the formula with power factor.