Discussion Overview
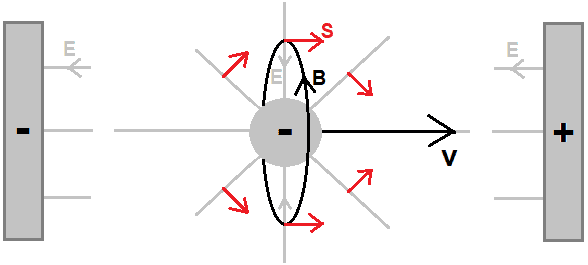
The discussion revolves around the behavior of the Poynting vector field in the context of a single electron moving between capacitor plates in free space. Participants explore the implications of the electron's electric field and the external electric field on the Poynting vector, particularly focusing on energy transfer and the nature of point particles.
Discussion Character
- Exploratory
- Technical explanation
- Debate/contested
Main Points Raised
- One participant questions the convergence of the Poynting vector field to the electron, suggesting that the expected behavior does not occur due to the dominance of the electron's electric field.
- Another participant asserts that the external electric field must be considered, implying that neglecting it leads to incorrect conclusions.
- There is a repeated emphasis on the infinite strength of the radial electric field close to the electron, raising questions about the significance of the finite external field.
- Some participants agree that work is done by the electric field on the electron, but they debate whether the Poynting vector should converge to the electron's location.
- A later reply introduces the idea that the Poynting vector must account for both the migration of the Coulomb field energy and the increase in the electron's kinetic energy, explaining the diffuse area of convergence.
- One participant notes the challenges posed by classical point particles and contrasts them with quantum approaches that allow for systematic treatment of divergences.
Areas of Agreement / Disagreement
Participants express differing views on the behavior of the Poynting vector in relation to the electron's electric field and the external field. While some agree on the necessity of considering both fields, there is no consensus on the implications of these considerations for the Poynting vector's behavior.
Contextual Notes
Participants highlight the limitations of classical point particle models and the complexities introduced by the interaction of electric fields. The discussion reflects unresolved questions about the nature of energy transfer in this scenario.
