- #1
Avimanyu Ray
- 17
- 1
Can we please look at the following attached file image?
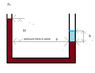
It shows a utube filled with a little water and the rest is oil.
Thus, the height of oil in one arm will be more than the height of water in the other.
When we compare the pressure at the height of the surface of water with that corresponding height of the oil, the pressures don't match. Why? Please refer to the attached image file.
It shows a utube filled with a little water and the rest is oil.
Thus, the height of oil in one arm will be more than the height of water in the other.
When we compare the pressure at the height of the surface of water with that corresponding height of the oil, the pressures don't match. Why? Please refer to the attached image file.