wakaranai
- 5
- 0
- Homework Statement
- Consider a superposition state |Ψ⟩ = (|2, 0, 0⟩ + |2, 1, 0⟩) of the hydrogen atom.
a) Calculate the probability density at t = 0 and sketch the function in the (xy) plane.
b) Calculate ⟨Ψ|r|Ψ⟩ and mark on the graph the expected value of the position obtained in part (a). Interpret your result.
- Relevant Equations
- I'm not certain about the equations
I did this and I don't know if it's correct:
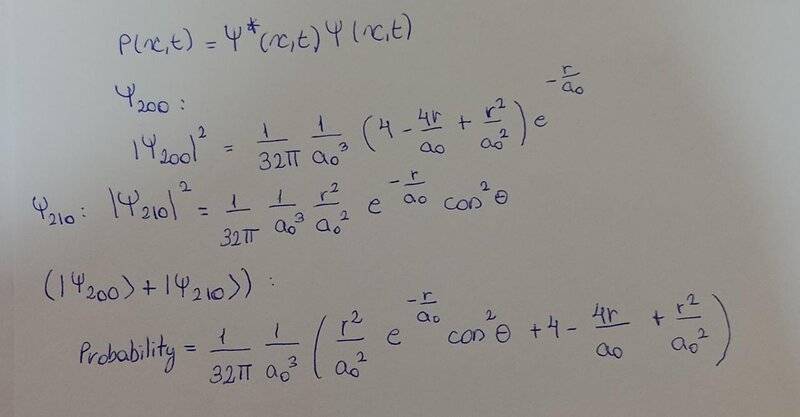
Last edited:
