Problem resolving forces into components

[yugeci]

I have problems with this question:

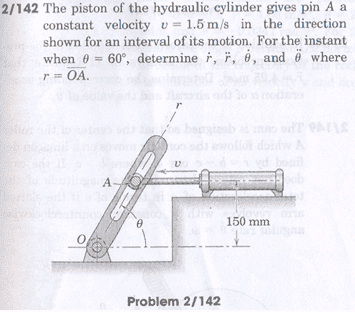
This is how I resolved v into its components (Vr and Vtheta):

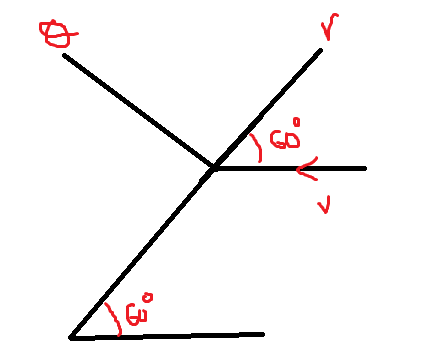
So with this I get
Vr = - V cos theta
Vtheta = V sin theta

However in my solution booklet the components are the other way around (Vr = - V sin theta, Vtheta = V cos theta) and I cannot figure out why. It makes no sense... am I right and the solution wrong?

 

[Khashishi]

The solution manual is wrong.

 

[FactChecker]

The extreme cases support you. When theta is small, (the piston is in line with the lever) almost all the change is in r and theta is almost constant. Conversely, when the lever arm is straight up (theta=90), r doesn't change and theta is the only thing changing. That puts the cos and sin where you have them.

 

[yugeci]

Thought so. Thanks. Another problem I have with the solution manual is that it says the magnitude of the total acceleration is zero and therefore the radial acceleration = angular acceleration (Ar = Atheta). Is this true? Because I thought the constant velocity only meant the tangential acceleration was zero... and there would be still be a normal acceleration equal to v^2 / r.

 

[Khashishi]

Either the solution manual is wrong again, or you have misread it somehow. $\ddot r$ and $\ddot theta$ have different units, so they can't be equal unless 0.