dGasim
- 16
- 0
Homework Statement
Hello,
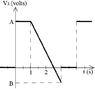
I am having problem solving this problem (picture below). The figure IS drawn to scale. A = 70 Volts
Q1. What is the numerical value of V(2) on the graph (in volts)?
Q2. What is the numerical value of point B on the graph (in volts)?
Q3. What is the period for the function V3?
Q4. What is the average for the function V3 (over one period of time)?
Homework Equations
f(x) = y0 + k(x-x0)
period = 2pi/n
The Attempt at a Solution
For the Q1 and Q2 I have tried to find the slope:
deltaX = x1-x0 = 2.5 - 1.0 = 1.5
deltaY = y1-y0 = 0 - 70 = -70
f(x) = 0 + (-70/1.5)(x-1.0)
f(2.0) = (-70/1.5)(1.0) = -70/1.5 (which is not correct)
I went the same way for Q2. If I understand Q1 i'll do Q2 very easily.
for Q3 and Q4 I don't know how to do them at all. How should I apply period function into this graph?
Thanks in advance,
Gasim Gasimzada