Problem with an Equation -- Solving for "a" in this large equation

[TheShermanTanker]

Ok, I know this may sound silly and I apologize for bringing in what should be a relatively easy equation. I'm trying to make the small a in the below equation the subject of the formula (That is, to push everything in the equation except a to one side of the equation and leave all the small letter a on the other side), but I'm getting stuck trying to do so halfway:

(Note: I'm trying to make the small letter a the subject of the formula, NOT the capital letter A's!)

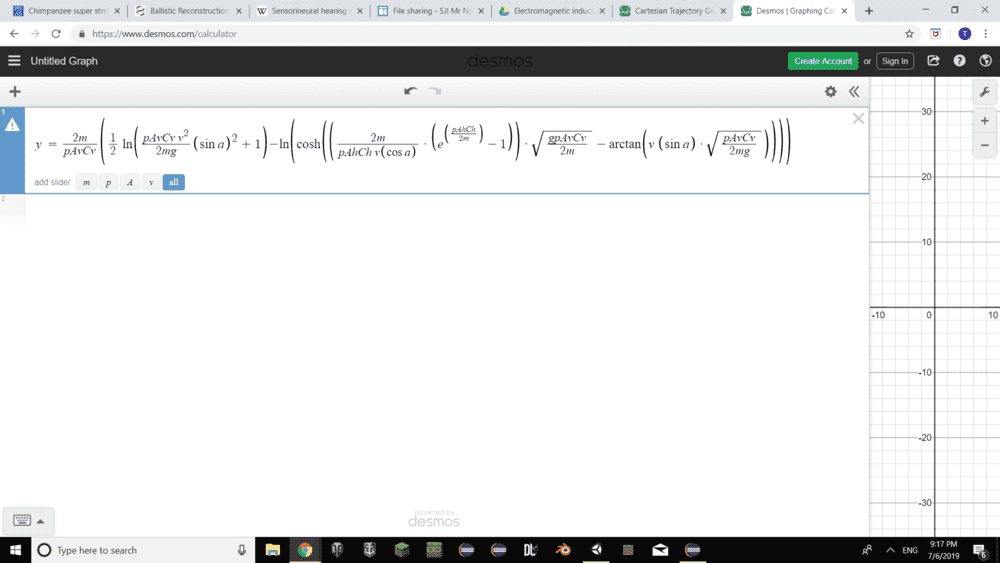
PS: The small dots you see in the equation are multiplication operators. They just mean this multiplied by this

Would appreciate any help for this! :)

 

[jedishrfu]

You could replace the many factors with a composite factor to reduce the equation to something a little more manageable:

$y = A ( (1/2)* ln ( B * sin^2(a) + 1) - ln ( cosh ( C / cos(a) ) * D - arctan ( v * sin(a) * E ) ) ) )$

where:

A = ...
B = ...
C = ...
D =  ( e^(...) - 1 )
E = ...

 

[Buzz Bloom]

Hi TheShemanTanker:

I think that Jedishrfu's suggestion is a good first step, although I would also eliminate v, including it in E. I suggest the following as a second step.

Take the exponential of both sides.

e^y = . . .

Hope this helps.

Regards,
Buzz