DDarthVader
- 51
- 0
Hello! I'm here again, now with a new exercise! 
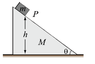
A block of mass m is at rest over this wedge (it's a triangle) of mass M that is at rest over a table. There is no friction. The point P of the block has a height h from the table. Then the block starts to move. What's the velocity of the wedge (triangle) when the point P hits the table? There is a picture from my textbook so you can see the situation.
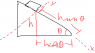
Well, since this exercise is from the Center of Mass chapter I tried to solve this by using center of mass. I know the coordinates of the center of mass they are ##x_{CM}## is ##2a/3## and that ##y_{CM}## is ##2b/3## (imagine a rectangle triangle). But the problem is that I have no ##b## or ##a## so I'm stuck. The only thing I was able to calculate was the velocity of the block when it hits the table ##\sqrt{2gh}=v## but it doesn't help at all. So, I'm stuck so I would like a hint to go on.
Thanks!
Homework Statement
A block of mass m is at rest over this wedge (it's a triangle) of mass M that is at rest over a table. There is no friction. The point P of the block has a height h from the table. Then the block starts to move. What's the velocity of the wedge (triangle) when the point P hits the table? There is a picture from my textbook so you can see the situation.
Homework Equations
The Attempt at a Solution
Well, since this exercise is from the Center of Mass chapter I tried to solve this by using center of mass. I know the coordinates of the center of mass they are ##x_{CM}## is ##2a/3## and that ##y_{CM}## is ##2b/3## (imagine a rectangle triangle). But the problem is that I have no ##b## or ##a## so I'm stuck. The only thing I was able to calculate was the velocity of the block when it hits the table ##\sqrt{2gh}=v## but it doesn't help at all. So, I'm stuck so I would like a hint to go on.
Thanks!