NicolaiTheDane
- 100
- 10
Homework Statement
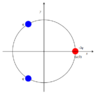
I'm suppose to set a general function of the electric field, at any point in the xy plane. As the picture shows, there are 2 point charges with 1 charge, and 1 point charge with -3 charge. Each of them are equally distanced from the origin, and all 3 are evenly spaced apart.
Homework Equations
I'm used Coulumbs law
The Attempt at a Solution
First I defined all the point charge locations, along with an arbitrary point, to represent the unknown point of the function.
Then I merely use Coumlumbs law, to add up all the expressions:
The final expression isn't pretty at all though:
The field as displayed by maple (if one fixes the fieldstrength, otherwise some arrows become very very small) looks like this:
Which to me looks about right. However the vector function isn't divergence free, which suggests I have messed up something. What am I doing wrong?
Attachments
-
 upload_2018-9-9_19-9-35.png3.6 KB · Views: 702
upload_2018-9-9_19-9-35.png3.6 KB · Views: 702 -
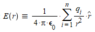 upload_2018-9-9_19-11-28.png1,001 bytes · Views: 323
upload_2018-9-9_19-11-28.png1,001 bytes · Views: 323 -
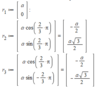 upload_2018-9-9_19-12-29.png2.4 KB · Views: 350
upload_2018-9-9_19-12-29.png2.4 KB · Views: 350 -
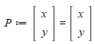 upload_2018-9-9_19-12-34.png513 bytes · Views: 355
upload_2018-9-9_19-12-34.png513 bytes · Views: 355 -
 upload_2018-9-9_19-13-8.png2.5 KB · Views: 342
upload_2018-9-9_19-13-8.png2.5 KB · Views: 342 -
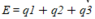 upload_2018-9-9_19-13-33.png546 bytes · Views: 346
upload_2018-9-9_19-13-33.png546 bytes · Views: 346 -
 upload_2018-9-9_19-14-16.png5.3 KB · Views: 355
upload_2018-9-9_19-14-16.png5.3 KB · Views: 355 -
 upload_2018-9-9_19-17-5.png23.4 KB · Views: 380
upload_2018-9-9_19-17-5.png23.4 KB · Views: 380