Problem with two pulleys and three masses

  • Thread starter Thread starter Erdi
  • Start date Start date
  • Tags Tags
    Pulley Pulleys
AI Thread Summary
The discussion revolves around a physics problem involving two pulleys and three masses, focusing on the tension in the strings and the motion of the masses. It is established that if mass M is zero, then mass m1 will accelerate downwards due to the weight of mass m2, which is heavier. The participants clarify that the tension in the string must equal the weight of m2, leading to a conclusion that if m1 is at rest, the system is not in equilibrium. The conversation emphasizes the importance of drawing free body diagrams and applying Newton's laws to understand the forces acting on each mass. Ultimately, the participants aim to derive expressions for tension and acceleration in the system, acknowledging the complexity of the interactions between the masses and the pulleys.
Erdi
Messages
37
Reaction score
6
Homework Statement
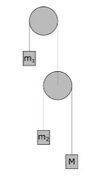
I cant figure out how to solve this task. I have got two pulleys, top pulley (A) and bottom pulley(B).
The pulley (A) is stuck to the wall and cannot move. The pulley B hangs in a thread and can
therefore moveup and down. Here m1 = 0.5 kg and m2 = 2.0 kg. Both pulleys can rotate freely. All
the pulleys can be are massless and there is no friction in the system.

How large must M be for m1 to be at rest?

Look at the figure.


Thanks for help!
Relevant Equations
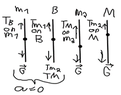
T1 - m1g = ma, where a = 0
I know that the tension from pulley B (T1) has to be equal the m*g of m1 for m1 to have acceleration = 0. But i can't figure how this works because the m2 is already heavier. And so the block(M) has to be negative weight?
 
Physics news on Phys.org
Heres the figure:
 

Attachments

  • Pulley.JPG
    Pulley.JPG
    3.2 KB · Views: 170
If M is zero which direction will m1 move? The problem is not a statics problem.
 
If M is zero, and also the pulley(b) is massless. Then the only thing weighing on the right side would be m2 that is 2kg. So the m1 that is 0.5kg would move upwards right?
 
What would (M=0) be the tension in the string if the pulleys are ideal and massless?
 
Are you thinking of the tension on the string T1 (on m1 from pulley B) or the tension on the string T2 (on M from m2) For in both cases i would say it is (T = m2g = 2*9.81 = 19.64N)
 
If M=0 then m1 will be accelerating down at g (there will be no constraint or T). If M is large then m1 will be accelerating up. Clearly somewhere in between m1 will have a=0
Draw a free body diagram for each mass and Newton for each . Put in the constraints from the pulley. Set a=0 for m1 (but not m2 m3)
 
  • Like
Likes scottdave
I may be wrong here, but i think youre confusing m1 with m2. Because the constraint on m1 is affected by the pulley(B) which is again affected by both m2 and M. So if M is zero, the m2 will still be 2kg. So the m1 will still be constrained by m2 that is 2kg even though M = 0kg.
Also here is the free body diagram i drawed:
 

Attachments

  • Free.png
    Free.png
    4.5 KB · Views: 151
In the original figure the mass M seems to be heavier than m2, that is why the tension on m2 is larger than the tension on M in the diagram.
 
  • #10
The tension in a massless rope is everywhere the same.
There are only two ropes.
G is not force
 
  • #11
Erdi said:
So the m1 will still be constrained by m2 that is 2kg even though M = 0kg.
No. The rope will have no Tension
 
  • #12
Alright i kinda get it because T2 = Mg = 0*9.81 = 0.
But what happens to the m2 then? It has a mass, what about the tension from that object?
 
  • #13
It falls. "Tension from an object" is not a thing.
 
  • #14
Write down Newton for m2 and for M
 
  • #15
I drawed a new figure if M was to be 0 in this situation. But so what your conclusion is that fr m1 to stay at rest. In this situation M has to be 0 then?
Pull.JPG
 
  • #16
hutchphd said:
Write down Newton for m2 and for M
Newton for m2: 19.62N
Newton for M (if M is 0kg): 0
 
  • #17
No that is not what I said. Reread#7
Erdi said:
Newton for m2: 19.62N
Newton for M (if M is 0kg): 0
My apologies for my shorthand I meant write down Newton's Law for m2 and M
 
  • #18
hutchphd said:
No that is not what I said. Reread#7

My apologies for my shorthand I meant write down Newton's Law for m2 and M
So Newtons 2.law is F = ma
Where F will be T - mg, so it is T - mg = ma
But since M is zero, the tension will be 0
So it is -mg = ma
For M that is ofcourse 0, but i don't understand m2
-m2*g = mM*a => -m2*g = 0, so the tension here will also be 0?
 
  • #19
For whatever it's worth, here is a different approach.
  1. Assume that the pulley on the right is attached to the ceiling. Find the tension ##T(M,m_2)## in the string connecting it to the ceiling as a function of ##M##, ##m_2## and ##g##.
  2. Answer the question, "if ##m_1## is at rest, what must the tension ##T_1## be in the string attached to it?"
  3. Set ##T_1 = T(M,m_2)## and solve for ##M##.
 
  • Like
Likes scottdave
  • #20
kuruman said:
For whatever it's worth, here is a different approach.
  1. Assume that the pulley on the right is attached to the ceiling. Find the tension ##T(M,m_2)## in the string connecting it to the ceiling as a function of ##M##, ##m_2## and ##g##.
  2. Answer the question, "if ##m_1## is at rest, what must the tension ##T_1## be in the string attached to it?"
  3. Set ##T_1 = T(M,m_2)## and solve for ##M##.
T_1 has to be equal the m1*g => 4.905N
T_m2 = 2*9.81 = 19.64
T_M = x
T_1 = T_M * T_m2 => 4.905 = 19.64 * M
T_M = 4.905 / 19.64 = 0.25N = 0.025kg?
Or did you mean T_1 = T_M + T_m2?
In that case T_M = 4.905 - 19.64 = -14.73N = -1.5kg??
 
  • #21
It is correct to say that ##T_1=m_1g##. You missed my point for the rest of what you have to do. The picture below shows a massless pulley attached to the ceiling and two unequal masses ##M## and ##m_2##. The first step is to find an expression for tension ##T_2## in terms of ##m_2## and ##M##. The second step is to set the expression equal to ##m_1g## and solve for ##M##.

Atwood.png

On Edit:
Tension ##T_1## mentioned above is the tension in the piece of the rope that is attached to mass ##m_1## as defined in item 2, post #19. It is not tension ##T_1## shown in the figure above. I am sorry for the unfortunate choice of subscripts and the confusion it might cause.
 
Last edited:
  • Like
Likes scottdave and erobz
  • #22
I like @kuruman approach fine.
I note that the title of the thread is incorrect and belies the problem. This system is not in equilibrium. Just be aware of the mis-statement please.
 
  • Like
Likes kuruman
  • #23
Yea.. the title got corrected incorrectly by an admin. Anyway tho. If only look at the system with pulley B attatched to a rope and start finding an expression for T2 in terms of m2 and M. Isnt the expression just:
T2 = T(m2 + M) like you wrote down above? So that M = T2 - m2?
 
  • #24
Erdi said:
Yea.. the title got corrected incorrectly by an admin. Anyway tho. If only look at the system with pulley B attatched to a rope and start finding an expression for T2 in terms of m2 and M. Isnt the expression just:
T2 = T(m2 + M) like you wrote down above? So that M = T2 - m2?
I did not write T2=T(m2+M). I wrote ##T_2=T(M,m_2)##. This means "find ##T_2## as a function of ##m_2## and ##M##." When one writes ##f(x)=x^2+3x##, one does not mean ##fx=x^2+3x##.
 
  • #25
Oh my bad. Right i don't know why i didnt mention it before, but i know that's how i get solution to answer. The problem is, i have searched a lot around. But i can't find the formula for what the tension for T2 will be when we have two masses m2 and M. I have looked at several videos and other questions, but i can't find the specific solution to find that expression..
 
  • #26
Erdi said:
Oh my bad. Right i don't know why i didnt mention it before, but i know that's how i get solution to answer. The problem is, i have searched a lot around. But i can't find the formula for what the tension for T2 will be when we have two masses m2 and M. I have looked at several videos and other questions, but i can't find the specific solution to find that expression..
Can you find an expression for ##T_1## in the figure in post #21? If so, how do you think ##T_1## is related to ##T_2##?
 
  • #27
T1 = mg + ma. And i guess that T2 is equal to T1 because the rope and is massless and the pulley are frictionless or something? In that case, could you please try to just give a very understandable reason why it is equal.
 
  • #28
Erdi said:
T1 = mg + ma. And i guess that T2 is equal to T1 because the rope and is massless and the pulley are frictionless or something?
If ##m_1## is not accelerating, is the lower pulley accelerating vertically? What does the answer to that imply about the force balance on that lower pulley?
 
  • #29
erobz said:
If ##m_1## is not accelerating, is the lower pulley accelerating vertically? What does the answer to that imply about the force balance on that lower pulley?
If m1 isn't accelerating the lower pully can't be accelerating vertically. Which implies that the force balance on the lower pulley will be in equalibrium?
 
  • Like
Likes erobz
  • #30
Erdi said:
If m1 isn't accelerating the lower pully can't be accelerating vertically. Which implies that the force balance on the lower pulley will be in equalibrium?
So the mass M is the same as m2 then?? M = 2kg?
 
  • #31
Erdi said:
So the mass M is the same as m2 then?? M = 2kg?
Slow down. You need some more things here. Do a FBD of the lower pulley. What are the forces acting on it? Remember you are isolating the pulley when you do this.
 
  • #32
The force acting on it will be T2 upward and m2 and M downwards
 

Attachments

  • Pull.JPG
    Pull.JPG
    5 KB · Views: 138
  • #33
Erdi said:
The force acting on it will be T2 upward and m2 and M downwards
##m_2## or ##M## aren't forces. You are to be "freeing" the pulley from all other bodies, severing the ropes. What are the forces acting to pull the pulley down. What is the force acting to pull the pulley upward? Are these forces balanced on the pulley?
 
  • #34
erobz said:
##m_2## or ##M## aren't forces. You are to be "freeing" the pulley from all other bodies, severing the ropes. What are the forces acting to pull the pulley down. What is the force acting to pull the pulley upward? Are these forces balanced on the pulley?
If that's the case, forces acting on it downwards is the gravitational force. BUT i don't understand what you mean with the upward force. Because you said to isolate the pulley, but you agreed that it wasnt accelerating (vertically at least) so the upward force is the same as downward force then? which is the gravitatioal force ??
 
  • #35
Erdi said:
If that's the case, forces acting on it downwards is the gravitational force. BUT i don't understand what you mean with the upward force. Because you said to isolate the pulley, but you agreed that it wasnt accelerating (vertically at least) so the upward force is the same as downward force then? which is the gravitatioal force ??
We are freeing the pulley from the other bodies. Not from the forces. What are the internal forces inside the rope that we expose when we "free" the pulley.
 
  • #36
erobz said:
We are freeing the pulley from the other bodies. Not from the forces. What are the internal forces inside the rope that we expose when we "free" the pulley.
Im sorry, I am lost. I really don't have a clue.
 
  • #37
Erdi said:
Im sorry, I am lost. I really don't have a clue.
Which forces are associated with the ropes?
 
  • #38
Originally, the pulley B and m1
 
  • #39
Erdi said:
Originally, the pulley B and m1
Lets back up. What are the forces acting on ##m_2##?
 
  • #40
That should be just the gravity and tension 1, tension 1= M*g
 
  • #41
Erdi said:
That should be just the gravity and tension 1, tension 1= M*g
##T_1 \neq Mg## That would be the case if ##M## or ##m_2## were NOT accelerating, but they are.

What is the force balance on ##m_2##
 
  • #42
its m2g
 
  • #43
Erdi said:
its m2g
Maybe I'm using confusing wording. That is just the force of weight. What is the sum of the forces acting on ##m_2##. I think you have already written this in an earlier post.
 
  • #44
If that's not T - mg = ma or just T - mg , then i really don't understand at all
 
  • #45
Erdi said:
If that's not T - mg = ma or just T - mg , then i really don't understand at all
Ok good:

$$T_1 - mg = ma$$

Now for the other mass ##M##?
 
  • #46
Thats also got to T1 - Mg = ma
 
  • #47
Erdi said:
Thats also got to T1 - Mg = ma
close. be careful about the coordinate system you chose. If ##m2## goes up is positive ##a## then what does that mean for the acceleration of ##M## here. Also, you used two different symbols for ##M##
 
  • #48
T1 + mg = ma?
 
  • #49
Erdi said:
T1 + mg = ma?
You chose a coordinate system where up was positive in #46 whether you did so intentionally or not. That is upward accelerations are positive. Upward forces are positive, downward forces are negative, downward accelerations are negative. Try again. And use a capital ##M## leave the little ##m##
 
  • #50
Well i think the formula is correct, so what you mean is:
T - Mg = M*(-a)
 

Similar threads

3 pulley problem with attached masses
Replies
15
Views
5K
Olympiad dynamics problem with 3 masses and a pulley
Replies
17
Views
2K
Newton's Second Law (Pulley Sustem)
Replies
3
Views
2K
Pulley system problem: 6 Pulleys and 1 Mass
Replies
5
Views
852
Accelerating pulleys (3 pulleys and 3 masses)
Replies
5
Views
2K
Using Effective Mass to find the accelerations of 3 masses connected by pulleys
Replies
25
Views
3K
Pulley with friction, how to get the friction in the pulley?
Replies
23
Views
2K
Analyzing acceleration of block on a ramp connected to a pulley
Replies
15
Views
1K
Problem with pulleys - two fixed and one movable
Replies
22
Views
299
Pulleys with Torque: Free Body Diagram Analysis
Replies
34
Views
3K

Hot Threads

Recent Insights

Back
Top