Tomas1337
- 13
- 1
So I'm working on an experiment where I do a projectile motion simulation here on Earth and want to know how it will fair in a low gravity environment such as in the moon with one common parameter in between, Force.
Imagine, here on earth, I have a mass that I push up with a force(F) for it to jump y meters. I record the mass, the height at which it reached and the time it took for it to reach that height which will then allow me to compute for my Force(F).
Now I want to know, if I used this same Force(F) on a different mass under a different gravity, how high it will reach?
I`ve come up so far with this.
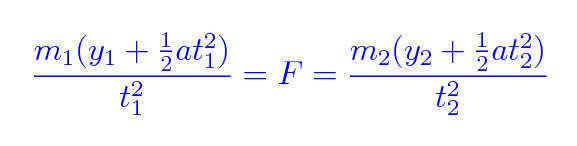
My problem is, when I do solve for the Force, I still have 2 missing parameters which is y and t which is preventing me from solving each variable. Any suggestions?
Imagine, here on earth, I have a mass that I push up with a force(F) for it to jump y meters. I record the mass, the height at which it reached and the time it took for it to reach that height which will then allow me to compute for my Force(F).
Now I want to know, if I used this same Force(F) on a different mass under a different gravity, how high it will reach?
I`ve come up so far with this.
My problem is, when I do solve for the Force, I still have 2 missing parameters which is y and t which is preventing me from solving each variable. Any suggestions?