Projectile Motion: Negative Launch Angles?

[mliuzzolino]

Hello everyone!

This is my first post, and I regret that it has to be a question that is so elementary.

The Problem:
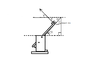
I am in an introductory engineering course in which we were divided into teams and told to construct a catapult. Rather than follow design requirements, and despite my protest, my team constructed a catapult the hurls our ping pong ball into the ground at angles that I refer to as negative launch angles.

Here is a link to a photo of our catapult and what's going on:
http://s872.photobucket.com/albums/ab287/uzzimike86/?action=view&current=FailedCatapult.png

I can never figure out how to get the photo to just load straight into the post. Sorry.

They are calling our launch angles 85, 100, and 115 degrees. They are referencing from the horizontal. Is this correct? In my mind I am thinking the launch angles are actually 5, -15, and -25 degrees.

The Question:
Are the launch angles 85, 100, and 115 degrees, or are the 5, -10, and -25 degrees?

I appreciate your time in reading through my situation and thanks in advance for any response that will settle this problem.

 

[Delphi51]

Welcome to PF!

Just to be clear, do you mean when the Θ in your diagram is 10 degrees, you say -10 and they say 100 degrees? I don't think 100 makes any sense at all, -10 makes some. What are you going to do with the angles? If you are going to take the flight of the ball after it bounces, then +10 would be the angle above horizontal that should be entered into the projectile motion formulas. Actually it would have to be 170 if you use the standard that positive x is to the right.

 

[Liquidxlax]

um when i see something like this you always start like

so negative would be going clockwise using the same values in reverse and negatives

 

[mliuzzolino]

Delphi51:

Thanks for the welcome!

Yes. When I say -10 degrees Θ is 10 degrees in the diagram.

Here is a less ambiguous sketch of our failed catapult and the situation:
http://s872.photobucket.com/albums/ab287/uzzimike86/?action=view&current=FailedCatapult-1.png

Am I incorrect to say that the launch angle is defined as the angle at which the object is projected at with respect to the horizon, and that it is not the angle at which the catapult arm makes with the horizon?

It appears as if they are referring to Θ as our launch angle, whereas I am saying that alpha is our launch angle. It seems to me that they are not referring to the launch angle at all - they are referring to the angle at which the arm makes with the horizon at the point of launch.

Sketch of a conventionally constructed catapult for reference:
http://s872.photobucket.com/albums/ab287/uzzimike86/?action=view&current=NormalCatapult.png

[Given the same conditions where Θ is angle that my team argues for as the launch angle and alpha being the angle that I claim is the launch angle.]

As we can see from the diagram (maybe not) and using elementary geometry concepts, Θ does not equal alpha (except at 45 degrees).

When one studies projectile motion and you are given a problem involving an angle, range, initial velocity, etc, the angle given as the launch angle is not Θ - it is alpha.

Now let's go back to the diagram of our failed catapult and use the same logic as that in the diagram of a conventional catapult.

If Θ is 85 degrees, alpha would be 5 degrees. If Θ is 100 degrees, alpha would be -10 degrees. If Θ is 115 degrees, alpha would be -25 degrees. The last two would be required to be negative angles in order to discern a difference between being launched downward at 10 degrees and being launch upward at 10 degrees, correct?

What we are going to be doing with the angles is using them in a technical report and a oral presentation. We will not have to be doing any calculations, which is fortunate considering the additional frustration I would experience with my lovely group.

Liquidxlax:
I understand what you are saying, but I just happened to draw the diagram from that perspective and I am just looking at it in a reversed fashion just so I don't have to redraw the diagram facing the other way.

I apologize for this extremely long-winded response, but I just want to make sure I understand this situation correctly.

 

[cjl]

From what I can see, you are almost definitely correct. The launch angle, as far as projectile motion is concerned, is the angle between the projectile velocity vector and the horizontal ( \alpha in your diagram).

 

[Liquidxlax]

From what I can see, you are almost definitely correct. The launch angle, as far as projectile motion is concerned, is the angle between the projectile velocity vector and the horizontal ( \alpha in your diagram).

alpha and theta should equal each other just that the angles are measured in different planes, yet the planes are parallel, which would equate to the two angles being equivalent

took me 5 tries... because i couldn't hit redo. BY SYMMETRY ALPHA EQUALS THETA!

 

[mliuzzolino]

Refer to this image:
http://s872.photobucket.com/albums/ab287/uzzimike86/?action=view&current=Projectile.png

Θ = the same angle that was denoted by Θ in previous diagrams.
α = the same angle that was denoted by α in previous diagrams.

Eq 1. δ = 90 - Θ
Eq 2. β = 90 - δ
Eq 3. α = 90 - β

Sub Eq 1. into Eq 2.
β = 90 - (90 - Θ)
β = 90 - 90 + Θ
Eq 4. β = Θ

Sub Eq 4. into Eq 3.
α = 90 - Θ

Therefore, α ≠ Θ

Returning to my situation. The group claims Θ, incorrectly as the launch angle, to be equal to 85 degrees. When Θ = 85, α = 5 which is proved algebraically above. When Θ = 100, α = -10; when Θ = 115, α = -25.

The only situation in which α = 90 - Θ would be the case in which Θ = 45.

I guess what I have come to the conclusion of is that Θ in this context is the angle of the catapult arm with respect to the horizon. This angle is not what is conventionally referred to as the launch angle.

 

[cjl]

alpha and theta should equal each other just that the angles are measured in different planes, yet the planes are parallel, which would equate to the two angles being equivalent

took me 5 tries... because i couldn't hit redo. BY SYMMETRY ALPHA EQUALS THETA!

They're related, but they aren't equal. They're complementary. \alpha + \theta = 90\deg This can be seen in your diagram too - look at the one I just uploaded.

\alpha + \beta = 90deg

\beta + \Theta = 90deg

\Theta = \alpha

\phi + \Theta = 90deg

\phi + \alpha = 90deg

\Psi = \phi

\Psi + \alpha = 90deg

Therefore psi and alpha (or, alpha and theta in the original labeling system) are complementary.

 

[Delphi51]

I get alpha = θ - 90
When alpha is 100 degrees, θ = 10 degrees. The 10 degrees is below horizontal as your alpha indicates.

 

[Liquidxlax]

They're related, but they aren't equal. They're complementary. \alpha + \theta = 90\deg This can be seen in your diagram too - look at the one I just uploaded.

\alpha + \beta = 90deg

\beta + \Theta = 90deg

\Theta = \alpha

\phi + \Theta = 90deg

\phi + \alpha = 90deg

\Psi = \phi

\Psi + \alpha = 90deg

Therefore psi and alpha (or, alpha and theta in the original labeling system) are complementary.

lol i shouldn't try to do this stuff at 1 am... i re did it with a few extra triangles and yes

alpha+theta = 90... my bad. Even without the triangles you can extend the alpha line to get a singular right angle triangle incorporating both alpha and theta