kkernodl
- 3
- 0
Homework Statement
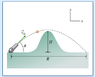
A projectile is fired with speed v0 at an angle θ from the horizontal as shown in the figure (see attachment).
Homework Equations
A. Find the highest point in the trajectory, H. Express the highest point in terms of the magnitude of the acceleration due to gravity g, the initial velocity v0, and the angle θ.
B. What is the range of the projectile, R? Express the range in terms of v0, θ, and g.
C. Find the angle theta above the horizontal at which the projectile should be fired. Express your answer in terms of H and R.
D. What is the initial speed? Express v0 in terms of g, R, and H.
E. Find tg, the flight time of the projectile. Express the flight time in terms of H and g.
The Attempt at a Solution
A. H=(v0sin(θ))2)/2g
B. R=v02sin(2θ)/g
C. I know that arctan(2H/R)=θ, however this isn't the correct answer. I've tried everything I can think of, but don't know how to solve this part.