Smart-Bunny
- 2
- 0
Hi everyone, , I just want to make sure if I have done the statements right. Thank you. :)
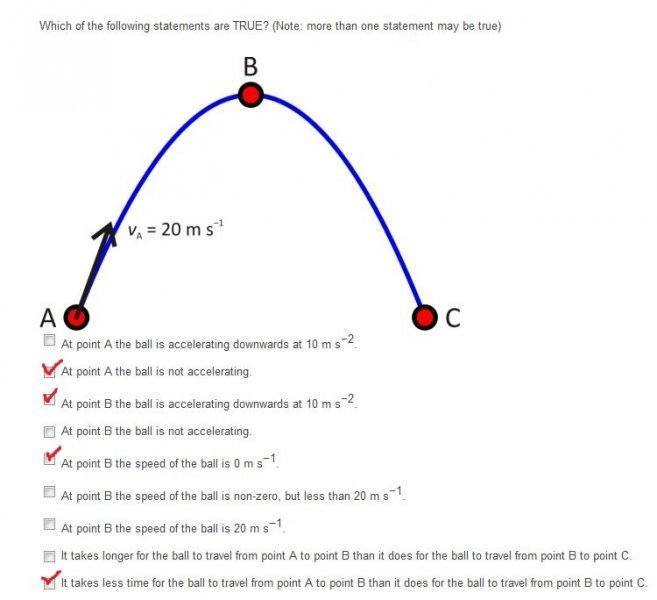
I concur.mrnike992 said:I've counted that one of your checks is correct so far, and that you are missing two others, for a total of three checked boxes. Other members, feel free to correct me if I am wrong.
All true.Smart-Bunny said:Thanks guys! At point A the ball accelerating downwards 10 m/s2, At point B the ball accelerating downwards 10 m/s2 and at point B the speed is non-zero but less than 20 m/s :)